Problem : Triangle Partitioning
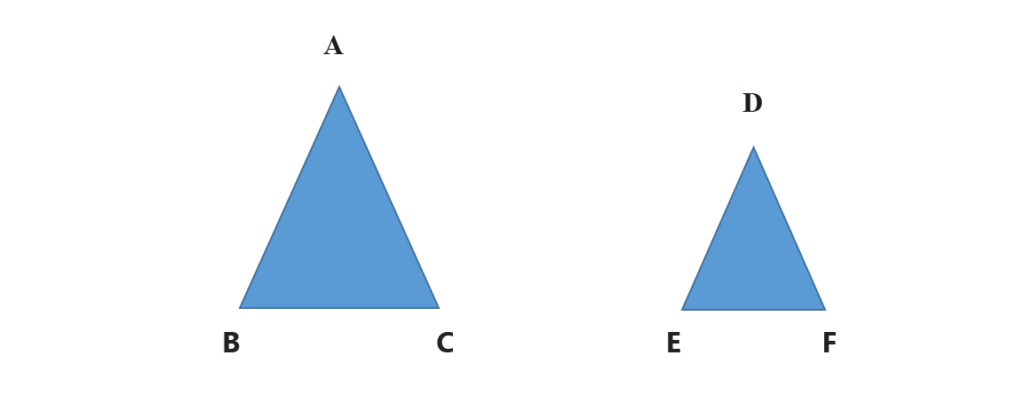
we know that , when two Triangle is identical triangles then they follow this criteria..
- The proportions of each of their arms will be equal to each other and the angles of each other will also be equal to each other.
- The area ratio of two identical triangles will be equal to the square ratio of their arms.
Here, triangle ABC and ADE is identical triangle.
So, the First criteria is,
DE / AB = AC / DF = EF / BC
and ∠A = ∠D and ∠B = ∠E and ∠C = ∠F
The Second criteria is,
△DEF / △ABC = (DE / AB)^2 = (AC / DF)^2 = (EF / BC)^2
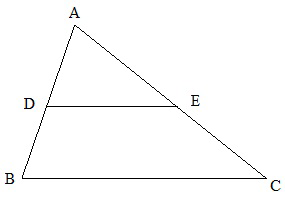
From the figure in question then we can write,
AD / AB = AE / AC = DE / BC ——————— (1)
and △ADE / △ABC = (AD / AB)^2 = (AE / AC)^2 = (DE / BC)^2 —————— (2)
From (2) we get,
△ADE / △ABC = (AD / AB)^2
AD = sqrt (△ ADE / △ ABC) * AB
Now, how do I get the values of △ADE and △ABC ?
In question, ratio = (△ADE / BDEC) is given. Thus, BDEC = 1.
We know that, △ABC = △ADE + BDEC
and △ADE = △ADE / BDEC
Here ,
△ADE =ratio and △ABC= ratio + 1.
So ,
New_ratio= ratio / (ratio + 1)
Cpp Code
#include <bits/stdc++.h>
#define Dpos(n) fixed << setprecision(n)
using namespace std;
int main()
{
int test_case;
cin >> test_case;
int i = 1;
while (test_case--)
{
double ab, ac, bc, ratio;
cin >> ab >> ac >> bc >> ratio;
double New_ratio = ratio / (ratio + 1);
cout << "Case " << i++ << ": " << Dpos(6) << ab*sqrt(New_ratio) << endl;
}
}
Python Code
import math
for test in range (int(input())):
ab,ac,bc,ratio=list(map(float ,input().split()))
New_ratio=ratio/(ratio+1)
print("Case {}:".format(test+1),math.sqrt(New_ratio)*ab)
Java Code
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int test = input.nextInt();
int i = 1;
while (i <= test) {
double ab = input.nextFloat();
double ac = input.nextFloat();
double bc = input.nextFloat();
double ratio = input.nextFloat();
double New_ratio= ratio/(ratio+1);
System.out.println("Case " + (i++) +": "+ Math.sqrt(New_ratio)*ab);
}
}
}
Tutorial source
 You are given AB, AC and BC. DE is parallel to BC. You are also given the area ratio between ADE and BDEC. You have to find the value of AD.
You are given AB, AC and BC. DE is parallel to BC. You are also given the area ratio between ADE and BDEC. You have to find the value of AD.

