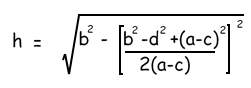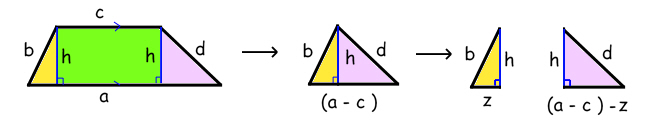Problem Name: Trapezium

LightOj-1178

Solution Approach:

Timothy Ti'en Ern Ang sent us a new trapezium area formula which uses Pythagoras.

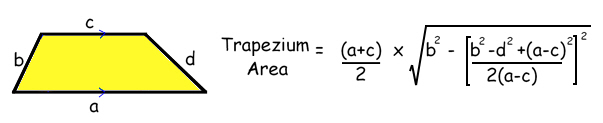
If you compare it to the original simple trapezium formula, you'll see he's found a way to work out the height h using the four sides.

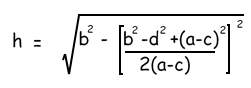
Here's how he did it!

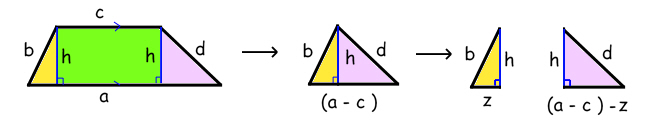
He took the two right-angled triangles off the end and put them together. We know the base of this triangle is (a-c). He then split them up.

If the base of one triangle is length z then the base of the other is (a-c)-z = (a-c-z).

For the first triangle, Pythagoras says:b^2= h^2 + z^2

For the second triangle:d^2 = h^2 + (a-c-z)^2

We'd like to know what z is, so as we have two simultaneous equations, we can subtract the second equation from the first equation to get rid of h . (Some people enjoy this sort of thing.)

b^2 - d^2 = z^2 - (a-c-z)^2

If we multiply the ugly thing at the end out we get

(a-c-z)^2 = (a^2 - ac -az -ca +c^2 + cz - za +zc + z^2)

which simplifies to (a^2 +c^2 +z^2 - 2ac -2az + 2cz )

We now put this in place of the (a-c-z)^2, not forgetting that there was a minus sign in front of the bracket...

b^2 - d^2 = z^2 - a^2 -c^2 -z^2 + 2ac +2az - 2cz

=> b^2 - d^2 = - a^2 -c^2 + 2ac +2az - 2cz

We now get everything without a z to the same side.

b^2 - d^2 + a^2 -2ac + c2 = 2az - 2cz

And now we conveniently notice that a^2 -2ac + c^2 factorises to (a-c)^2, and the other side factorises too.

b^2 - d^2 + (a-c)^2 = 2z(a-c)

Divide through by 2(a-c), swap the sides over and we've got a value for z. BINGO!

z = [ b^2 - d^2 + (a-c)^2 ] / 2(a-c)

At this point it's helpful to work out what z^2will be:

z^2 = [b^2 - d^2 + (a-c)^2 ]^2 /[2(a-c)]^2

All we do now is go back to our first Pythagoras triangle equation and twiddle it round so we get h^2 = b^2 -z^2 and then put in the z^2 value we just worked out.

h^2 = b^2 - [b^2 - d^2 + (a-c)^2 ]^2 / [2(a-c)]^2

Take a square root of both sides and we get...

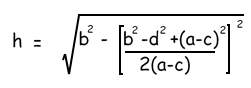
• Time Complexity: O(1) per test case.

Note : Reference source murderousmaths.co.uk

Cpp Code

#include <bits/stdc++.h>
#define Dpos(n)    fixed<<setprecision(n)
using namespace std;
int main()
{

    int test;
    cin >> test;
    int i=1;
    while (test--)
    {
         double a,b,c,d;
         cin>>a>>b>>c>>d;
         double value=(b*b - d*d +(a-c)*(a-c))/(2*(a-c));
         double area= (a+c)*0.5*sqrt(b*b - value*value);
         cout<<"Case "<<(i++)<<": "<<Dpos(6)<<area<<'\n';
    }


}

Python Code

import math
for test in range(int(input())):
    a,b,c,d=list(map(float , input().split()))
    value=(b*b - d*d +(a-c)*(a-c))/(2*(a-c));
    area=(a+c)*0.5* math.sqrt(b*b- value*value)
    print("Case {}: {}".format(test+1 , area))

Happy Coding!

Written by : Md. Rasel Meya

---

Tutorial source