LOJ 1398 - Winger Trial
Keywords: Flows, Min-Cut
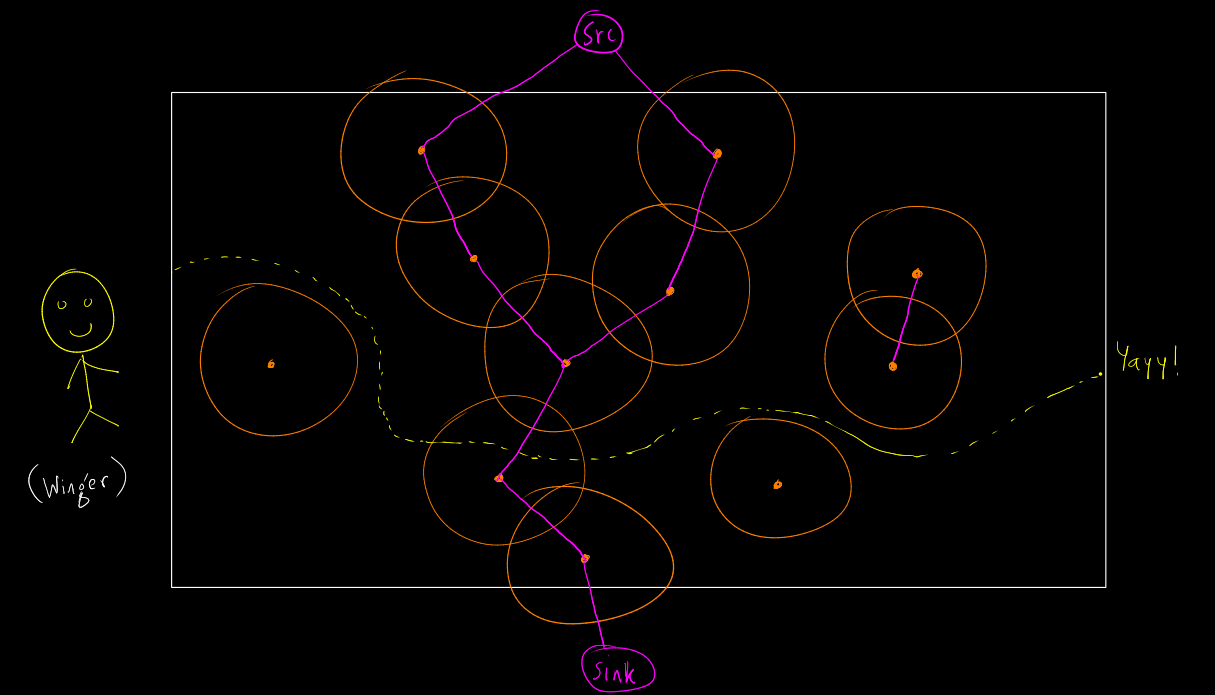
Consider a circle for each of the robots. Let's consider vertices for the circles. We shall add two more vertices, source and sink. Let's do the following:
- Split each vertex except source, sink into two vertices. Suppose i'th vertex is split into a_i and b_i. Add an edge a_i -> b_i.
- If a circle intersects or touches with the top side border of the field (y=W), then we shall add an edge from source to the corresponding vertex for the circle. Since the vertex is split into two, we'll add source -> a_i.
- If a circle intersects or touches with the bottom side border of the field (y=0), then we shall add an edge from the corresponding vertex for the circle to the sink. Since the vertex is split into two, we'll add b_i -> sink.
- If two circles intersect or touch, we shall add an edge between their corresponding vertices. Again, since the vertices are both split, we shall add b_i -> a_j and b_j -> a_i edges.
- Each edge will have capacity = 1.
For mentioned source and sink, the value of the minimum cut will be our result.
How?
The edges represent "some kind of wall". Between source and sink, that is, between the top and bottom side borders, there are some hierarchy of walls. We shall try to minimize the number of walls we have to run through to get from the left side to the right side. Thus, the minimum cut value.
Questions to ask
- Why do we need to split the vertices?
- Should we have given capacity = 2 when adding edges between vertices for circles i and j?
- What happens when there's a path from left to right without touching any of the circles?
Following is a rough illustration without the vertex-splitting:
C++ Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define ff first
#define ss second
#define INF 2000000000
const int MAX_E=20409;
const int MAX_V=209;
int ver[MAX_E],cap[MAX_E],nx[MAX_E],last[MAX_V],ds[MAX_V],st[MAX_V],now[MAX_V],edge_count,S,T;
inline void reset()
{
memset(nx,-1,sizeof(nx));
memset(last,-1,sizeof(last));
edge_count=0;
}
inline void addedge(const int v,const int w,const int capacity,const int reverse_capacity)
{
ver[edge_count]=w; cap[edge_count]=capacity; nx[edge_count]=last[v]; last[v]=edge_count++;
ver[edge_count]=v; cap[edge_count]=reverse_capacity; nx[edge_count]=last[w]; last[w]=edge_count++;
}
inline bool bfs()
{
memset(ds,-1,sizeof(ds));
int a,b;
a=b=0;
st[0]=T;
ds[T]=0;
while (a<=b)
{
int v=st[a++];
for (int w=last[v];w>=0;w=nx[w])
{
if (cap[w^1]>0 && ds[ver[w]]==-1)
{
st[++b]=ver[w];
ds[ver[w]]=ds[v]+1;
}
}
}
return ds[S]>=0;
}
int dfs(int v,int cur)
{
if (v==T) return cur;
for (int &w=now[v];w>=0;w=nx[w])
{
if (cap[w]>0 && ds[ver[w]]==ds[v]-1)
{
int d=dfs(ver[w],min(cur,cap[w]));
if (d)
{
cap[w]-=d;
cap[w^1]+=d;
return d;
}
}
}
return 0;
}
inline long long flow()
{
long long res=0;
while (bfs())
{
for (int i=0;i<MAX_V;i++) now[i]=last[i];
while (1)
{
int tf=dfs(S,INF);
res+=tf;
if (!tf) break;
}
}
return res;
}
int l, w, n, d;
pii c[MAX_V];
inline bool lineCircleSects(int i, int b) {
int up = c[i].ss+d, down = c[i].ss-d;
if(up < b or down > b) return false;
int left = c[i].ff-d, right = c[i].ff+d;
if(left > l or right < 0) return false;
return true;
}
inline bool circleIntersects(int i, int j) {
ll dis2 = (ll)(c[i].ff-c[j].ff)*(ll)(c[i].ff-c[j].ff) + (ll)(c[i].ss-c[j].ss)*(ll)(c[i].ss-c[j].ss);
return dis2 <= d*d*4LL;
}
int main() {
int t, tc=0;
scanf("%d", &t);
while(t--) {
scanf("%d %d %d %d", &l, &w, &n, &d);
for(int i=1; i<=n; ++i) scanf("%d %d", &c[i].ff, &c[i].ss);
reset();
S = 0, T = n+n+1;
for(int i=1; i<=n; ++i) {
addedge(i, i+n, 1, 0);
if(lineCircleSects(i, w)) addedge(S, i, 1, 0);
if(lineCircleSects(i, 0)) addedge(i+n, T, 1, 0);
for(int j=i+1; j<=n; ++j) {
if(!circleIntersects(i, j)) continue;
addedge(i+n, j, 1, 0);
addedge(j+n, i, 1, 0);
}
}
ll res = flow();
printf("Case %d: %lld\n", ++tc, res);
}
return 0;
}
reborn++
Dec 13 2020
Tutorial source

