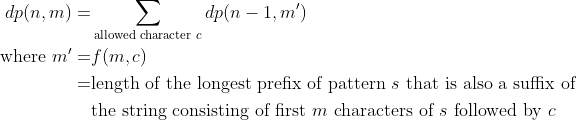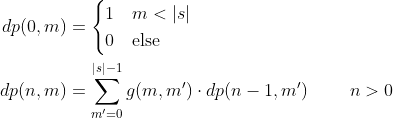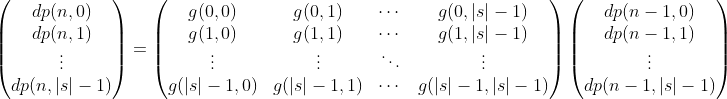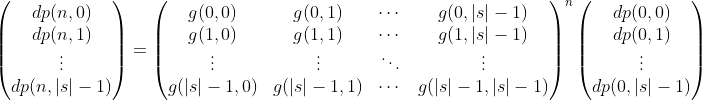LightOJ 1268 - Unlucky Strings
keywords: dp, matexpo, kmp
You are asked to find the number of strings of length n consisting of some restricted lowercase letters which doesn't contain a certain pattern s.
Solution
TL, DR; establish a recurrence for the solution and find out the n'th term using matrix exponentiation.
Let's define dp(n, m) to be the number of such strings of length n that do not contain pattern s and have the first m characters of s prepended to the left of these n characters.
We can think such strings to be of length m + n with the first m characters being the first m characters of s.
For example, suppose s = "abc". dp(3, 2) will refer to those string of the form a b _ _ _.
The first 2 characters are that of s, and any characters can be put in place of those underscores as long as the resulting strings do not contain abc as a sub-string.
So, abacb can be referred by dp(3, 2) while abcab shouldn't since it contains abc as a substring.
Similarly, for s = "abc", dp(5, 1) may refer to those string of the form a _ _ _ _ _ while dp(4, 0) may refer to _ _ _ _.
We can define dp(0, m) = 1 for any m < |s| and to have value 0 elsewise.
This is because, if we are left with no positions to put characters in to make a string, we must depend on how many characters has been matched with the pattern so far in the past (that is m).
And since we don't like the pattern to be included, we can't let all the pattern to be matched. So, m must be less than |s| to produce a desired string.
Onto the transitions, how do we produce dp(n, m) given the values of dp(n - 1, m')?
Suppose, s = "abac", the allowed characters are a, b, c, d, and we are trying to figure out dp(4, 3). We can consider those strings to be similar to a b a _ _ _ _.
Let's put a character at the first underscore.
- If we put
a there, it becomes a b a a _ _ _. 3 places remaining to fill, and if we notice carefully only 1 character matches with a prefix of s, the last a that we put.
So the number of characters put immediately to the left that matches with s from the beginning is 1, i.e. m = 1.
We might write this string as a _ _ _ which refers to dp(3, 1).
- If we put
b there, it becomes a b a b _ _ _. Again 3 places remaining to fill but this time 2 characters match with a prefix of s, the last a b.
So, m = 2, n = 3 for the new string which we can write as a b _ _ _.
- For
c however, it becomes a b a c _ _ _. Note that all 4 characters to the left matches with s and thus this shouldn't be allowed.
We simply ignore this case.
- If we put
d, it becomes a b a d _ _ _. No suffix of abad matches with any prefix of s.
So, this produces dp(3, 0) similar to _ _ _.
We conclude that for this example, dp(4, 3) = 1 * dp(3, 1) + 1 * dp(3, 2) + 1 * dp(3, 0). In a general case, for n > 0, we can write
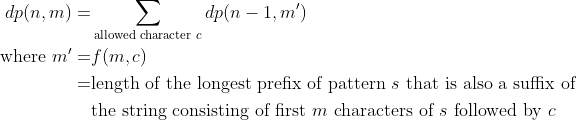
We can compute f(m, c) by using the KMP Prefix Function or by simple brute-force.
In our previous example, f(3, 'a') = 1, f(3, 'b') = 2, f(3, 'c') = 4, f(3, 'd') = 0.
Let's define g(m, m') as the number of allowed characters c for which f(m, c) = m'.
In the previous example,
g(3, 0) = 1 (for character 'd')
g(3, 1) = 1 (for character 'a')
g(3, 2) = 1 (for character 'b')
g(3, 3) = 0 (no such character)
So we can define dp(n, m) by the following:
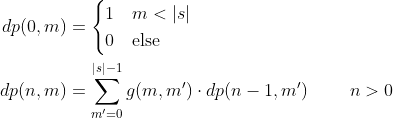
Using matrices, we can write:
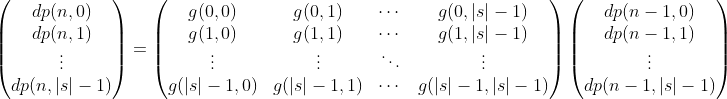
Since, g(m, m') is constant, the square matrix in the middle remains constant. Thus
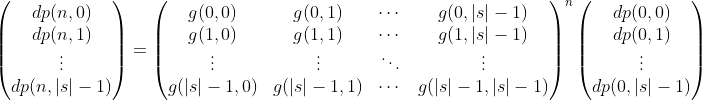
Using matrix exponentiation, we can find dp(n, 0) for a given n in O(|s|^3 lg n) time.
C++ Implementation
Notes
- Modulo by
2^32 can be simply done by using unsigned int data type.
#include <bits/stdc++.h>
using namespace std;
struct Mat {
const static int SZ = 57;
int row, col;
unsigned int v[SZ][SZ];
Mat(int r=0, int c=0) {
row = r, col = c;
memset(v, 0, sizeof v);
}
Mat operator * (const Mat &p) const {
assert(col == p.row);
Mat ret(row, p.col);
for(int i=0; i<ret.row; ++i) {
for(int j=0; j<ret.col; ++j) {
unsigned int& sum = ret.v[i][j];
for(int k=0; k<col; ++k) {
sum += v[i][k] * p.v[k][j];
}
}
}
return ret;
}
Mat power (int p) {
assert(row == col);
Mat base = *this;
Mat ret(row, col);
for(int i=0; i<row; ++i) ret.v[i][i] = 1;
while(p > 0) {
if(p & 1) ret = ret * base;
base = base * base;
p >>= 1;
}
return ret;
}
};
vector<int> prefix_function(string P) {
vector<int> pi(P.size());
pi[0] = 0;
int q = 0;
for(int i=1; i<(int) P.size(); ++i) {
while(q > 0 and P[q] != P[i]) q = pi[q-1];
if(P[q] == P[i]) ++q;
pi[i] = q;
}
return pi;
}
int f(int m, char c, const string& s, const vector<int>& pi) {
while(m > 0 and s[m] != c) m = pi[m - 1];
if(s[m] == c) ++m;
return m;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t, tc = 0;
cin >> t;
while(t--) {
int n;
cin >> n;
string alphabet;
cin >> alphabet;
string s;
cin >> s;
auto pi = prefix_function(s);
int ns = s.size();
Mat G(ns, ns);
for(int m=0; m<ns; ++m) {
for(char c : alphabet) {
int m_prime = f(m, c, s, pi);
if(m_prime < ns) G.v[m][m_prime] += 1;
}
}
G = G.power(n);
Mat base(ns, 1);
for(int m=0; m<ns; ++m) {
base.v[m][0] = 1;
}
Mat dp_n = G * base;
unsigned int res = dp_n.v[0][0];
cout << "Case " << ++tc << ": " << res << "\n";
}
return 0;
}
reborn++
Jan 14 2021
Tutorial source