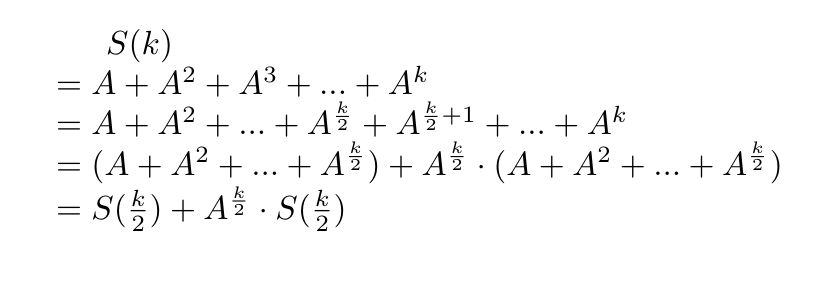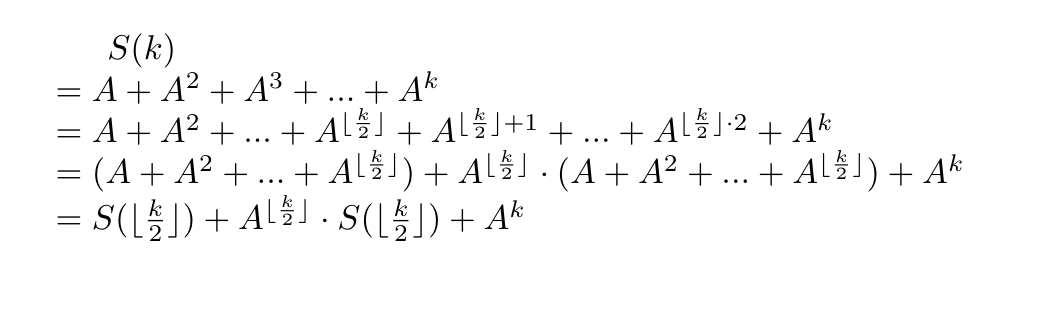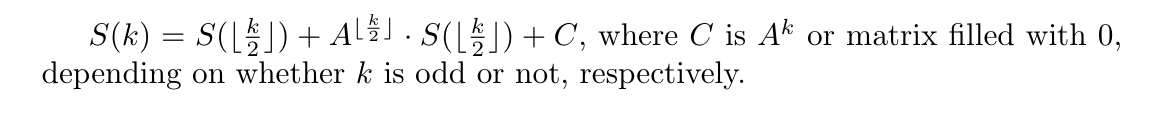1142 - Summing Up Powers (II)

Problem Specification

The problems asks you to find A+A^2+A^3+...+A^k for a given A and k, where A is an n x n matrix and k is an integer (1 <= n <= 30, 1 <= k <= 10^9). There are at most 20 test cases, and you have to print only the last digit for every cell of the matrix.

Some discussions and insights

Without any time limit, the problem looks very simple. Starting with A, you keep adding it to the result and keep multiplying it with A. But it obviously fails because the time complexity becomes O(k * n^3). Hmm. That's a problem. Let's try to solve some different problems related to this.

Hint 1

Can you find A^k only, for the same constraints, in O(logk * n^3) time? If you can't, you might want to learn about it from this link. Our problem directly needs this knowledge.

Hint 2

Let's assume you can find A^k using modular exponentiation (commonly known as bigmod). Have you noticed how exactly bigmod works, or how it does what it does? Can we do something similar here?

Solution

Let, S(k) = A+A^2+A^3+...+A^k.

Case 1: k is even

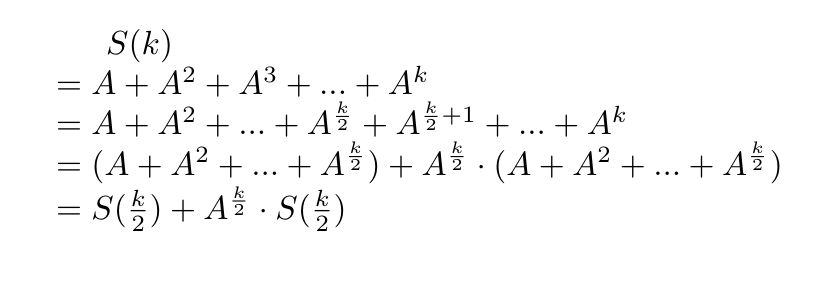
Isn't this recurrence beautiful? :sparkles: To find S(k), you can solve for S(k/2), find A^(k/2) in O(logk * n^3) time using modular exponentiation, do necessary calculation and produce the result. but what about when k is odd? Can you find it similarly?

Case 2: k is odd

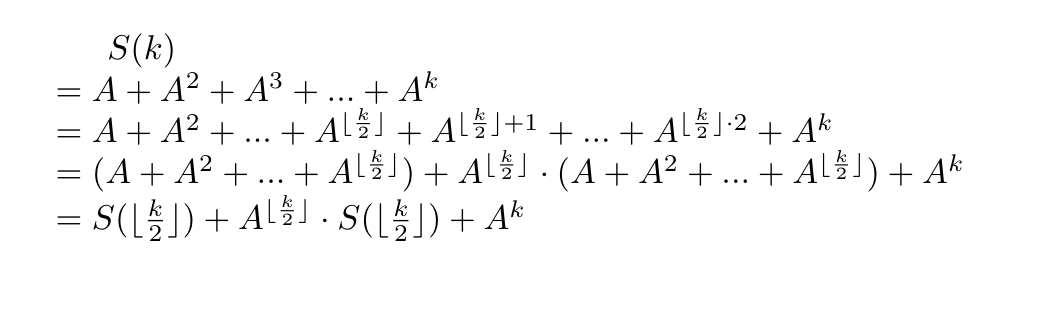
So, it looks like the case is very similar for both the cases. In short,

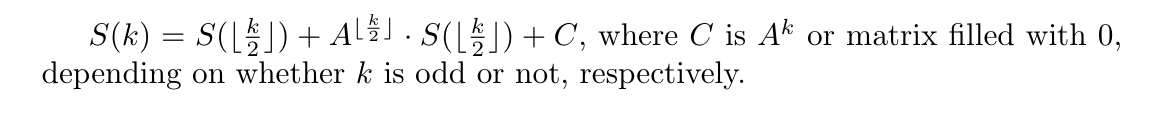
The overall time complexity becomes O( (log k)^2 * n^3).

Code in C++

#include <bits/stdc++.h>
#define ffr(i,a,b) for(i=a;i<b;i++)
#define mm(a,b) memset(a,b,sizeof(a))
#define pii pair<int,int>
#define plolo pair<ull,ull>
#define xx first
#define yy second
#define mp make_pair
using namespace std;

// necessary matrix class
class matrix
{
public:
    int r, c;
    int arr[52][52];
    matrix(){}
    matrix(int rr, int cc)
    {
        r=rr; c=cc;
        int i, j;
        ffr(i,0,r) ffr(j,0,c) arr[i][j]=0;
    }

    void print()
    {
        int i, j;
        ffr(i,0,r)
        {
            ffr(j,0,c)
            {
                cout << arr[i][j];
            }
            cout << endl;
        }
    }
    matrix operator + (const matrix &b) const
    {
        int i, j;
        matrix niu(r,c);
        ffr(i,0,r)
        {
            ffr(j,0,c)
            {
                int temp = arr[i][j]+b.arr[i][j];
                if(temp>=10) temp-=10;
                niu.arr[i][j] = temp;
            }
        }
        return niu;
    }
    matrix operator * (const matrix &b) const
    {
        int i, j, p;
        int sum;
        matrix niu(r, b.c);
        ffr(i,0,r)
        {
            ffr(j,0,b.c)
            {
                sum=0;
                ffr(p,0,c)
                {
                    int temp = arr[i][p]*b.arr[p][j];
                    sum+=temp;
                }
                niu.arr[i][j]=sum%10;
            }
        }
        return niu;
    }
};

// modular exponentiation for matrix 

matrix bigMod(matrix x, int n)
{
    matrix res(x.r,x.c);
    bool unassigned=1;
    while (n>0)
    {
        if (n&1)
        {
            if(unassigned) res=x;
            else res = x*res ;
            unassigned=0;
        }
        x = x*x ;
        n >>= 1;
    }
    return res;
}

// Described S(k) function  in the recurrence
matrix func(matrix A, int k)
{
    if(k==0)
        return matrix(A.r,A.c);
    matrix ans(A.r,A.c), fn2 = func(A,k/2), ak2 = bigMod(A,k/2);
    if(k&1)
        ans=bigMod(A,k);
    return ans + fn2 + ak2*fn2;
}

/*

fk = a + a^2 + a^3 + ... a^k
   = f(k/2) + a^(k/2) . f(k/2) + (k is odd)? a^k:0

*/

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int cc=1, tt; cin >> tt;
    while(tt--)
    {
        int k, N, i, j, x;
        cin >> N >> k;
        matrix A(N,N);
        ffr(i,0,N)
        {
            ffr(j,0,N)
            {
                cin >> x;
                if(x==10) x=0;
                A.arr[i][j]=x;
            }
        }
        matrix S = func(A,k);
        cout << "Case " << cc++ << ":\n";
        S.print();
    }
}

---

Tutorial source