You are a rich man, and recently you bought a place which contains some mines of rare minerals like gold, platinum, etc. As they are rare, they are expensive. Thus, you want to protect them from thieves. But things are not as easy as it looks.

You hired a group of engineers to make some wired fences around the mines. As they were just engineers (not problem solvers!), they drilled some holes in random places. The idea was to put some pillars on the drilled holes and some wires would be wrapped around the pillars where wires would be placed between any two pillars in straight lines. Finally, electrifying the wires would solve the problem. In this way, each mine would be surrounded by a fence.

But the engineers drilled the holes in positions such that some of the mines might not be covered by any fences. So, you have planned that you would put some guards in those mines that are not surrounded by any fence. To guard a single mine, it would cost you G dollars, and a pillar would cost you P dollars. As you are a rich man, the costs of wires are negligible.

Now, you want to put guards in some mines and surround some other mines with fences using the pre-drilled holes, you want to find the optimal cost to protect everything. The fences may or may not be convex.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing four integers N(3 ≤ N ≤ 100), M (1 ≤ M ≤ 100), G (1000 ≤ G ≤ 2000) and P (100 ≤ P ≤ 200), N denotes the number of pre-drilled holes, and M denotes the number of mines.

This line is followed by N lines that describe the positions of the holes, and then by M lines that describe the positions of the mines. All positions are given as pairs of integers x y on one line (0 ≤ x, y ≤ 1000). You can assume that no two positions (of holes and mines) coincide and that no three positions are collinear.

Output

For each case, print the case number and the minimum cost to protect all the mines.

Sample

Sample Input	Sample Output
Click to copy 2 7 6 1000 100 0 0 20 0 1 10 39 10 1 20 39 20 20 30 3 9 37 9 3 21 37 21 18 24 50 24 4 3 1500 100 0 0 0 10 10 0 10 10 5 4 4 1 8 6	Click to copy Case 1: 1600 Case 2: 300

Notes

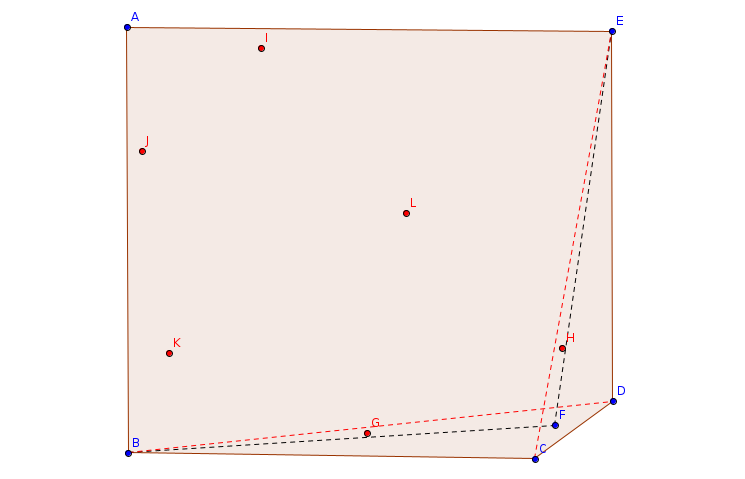
In the bird's eye view, we can get the following figure for sample 1. There are seven pre-drilled holes (marked as circles), and six mine positions (marked as squares). The straight lines show the wires and the closed regions from the fences. The figure shows one of the optimal solutions.

Mine Positions

LightOJ 1313 - Protect the Mines

Keywords: Convex-Polygons, Shortest-Path

Solution

Given the constraints, it is always better to cover a mine with poles instead of guards if possible. Because:

Guard cost G is at least 5 times bigger than pole cost P.
If a mine can be fenced around, it can be done so with no more than 3 poles.

Some mines may not be fenced altogether, because there may be no 3 poles that cover it. These mines will lie outside of the convex hull generated from the pole points. Why?

So, now we have a set of mine points all of which we want to fence, using some pole points. And we want to minimize the number of pole points we use.

We can make the following claims:

Instead of separate fences, we can make a single fence using the same or less number of poles yet fencing the same or more number of mines.

We can turn a concave fence into convex reducing the number of poles used by at least one yet fencing the same or more number of mines.

Thus, our task comes down to creating a convex polygon with the smallest number of vertices (pole points) that can cover all the mines. (Of course, the mines that cannot be covered at all are ignored.)

We can turn this into a graph problem. Let's consider vertices for every pole points. We will add an edge from u to v if all the mines are on the left side of vector p_v - p_u where p_u, p_v are corresponding pole points. (A point P is said to be on the left side of a vector AB if the cross product of vector AB and AP is positive.)

The vertices on the shortest cycle in this directed graph are indeed the pole points forming a convex polygon covering all the mine points. We can find the shortest cycle length using Floyd-Warshall algorithm. (or any shortest path algorithm)

Total complexity: O(N^3 + MN^2)

A Flawed Approach

Assuming the smallest convex polygon that covers all the mine points, can be made from the convex hull of the given pole points sometimes produce an worse result. An example figure is given below:

ABCDE is our convex hull. We cannot cover all the red points with ABDE or ABCE. But we can cover them all with a 4-side polygon ABFE where F is not on the convex hull, rather inside.

C++ Code:

#include <bits/stdc++.h>

using namespace std;

typedef int Ti;

const int inf = 0x3f3f3f3f;

typedef struct Pt {
    Ti x, y;
    Pt(Ti x = 0, Ti y = 0) : x(x), y(y) { }

    bool operator < (const Pt& p) const { return x == p.x ? y < p.y : x < p.x; }
    bool operator == (const Pt& p) const { return x == p.x and y == p.y; }

    Pt operator - (const Pt& p) const { return Pt(x - p.x, y - p.y); }
} Vec;

Ti cross(Vec a, Vec b) { return a.x * b.y - a.y * b.x; }

int ccw(Pt a, Pt b, Pt c) { return clamp(cross(b - a, c - a), -1, 1); }

typedef vector<Pt> Poly;

Poly convex_hull(Poly p) {
    sort(p.begin(), p.end());
    Poly h;
    for(int i = 0; i < 2; ++i) {
        auto k = h.size();
        for(Pt pt : p) {
            while(h.size() > k + 1 and ccw(h[h.size() - 2], h.back(), pt) <= 0)
                h.pop_back();
            h.push_back(pt);
        }
        h.pop_back();
        reverse(p.begin(), p.end());
    }
    return h;
}

int point_in_convex_polygon(Pt o, const Poly& p) {
    int n = p.size(), l = 1, r = n - 1;
    while(l + 1 < r) {
        int m = (l + r) / 2;
        if(ccw(p[0], p[m], o) > 0) l = m;
        else r = m;
    }
    int d1 = ccw(p[0], p[l], o), d2 = ccw(p[l], p[r], o), d3 = ccw(p[r], p[0], o);
    if(d1 < 0 or d2 < 0 or d3 < 0) return 1;    // OUTSIDE
    if(o == p[0] or !d2 or (l == 1 and !d1) or (r == n - 1 and !d3)) return 0;    // ON PERIMETER
    return -1;    // INSIDE
}

bool points_on_left(const Poly& p, Pt a, Pt b) {
    for(const Pt& pt : p) {
        if(ccw(a, b, pt) < 0) return false;
    }
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int t, tc = 0;
    cin >> t;

    while(t--) {
        int n, m, guard_cost, pole_cost;
        cin >> n >> m >> guard_cost >> pole_cost;

        Poly p(n), mines(m);
        for(Pt& pt : p) cin >> pt.x >> pt.y;
        for(Pt& pt : mines) cin >> pt.x >> pt.y;

        int res = 0;

        Poly outer = convex_hull(p);
        Poly inner;
        for(const Pt& pt : mines) {
            if(point_in_convex_polygon(pt, outer) > 0) {
                res += guard_cost;
            }
            else {
                inner.push_back(pt);
            }
        }

        if(!inner.empty()) {
            inner = convex_hull(inner);
            vector<vector<int>> d(n, vector<int>(n, inf));

            for(int i=0; i<n; ++i) {
                for(int j=0; j<n; ++j) {
                    if(i != j and points_on_left(inner, p[i], p[j])) {
                        d[i][j] = 1;
                    }
                }
            }

            for(int k=0; k<n; ++k) {
                for(int i=0; i<n; ++i) {
                    for(int j=0; j<n; ++j) {
                        d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
                    }
                }
            }

            int poles = inf;
            for(int i=0; i<n; ++i) poles = min(poles, d[i][i]);
            res += poles * pole_cost;
        }

        cout << "Case " << ++tc << ": " << res << "\n";
    }

    return 0;
}

reborn++
May 2, 2021

Tutorial source