Two players, Alice and Bob are playing a strange game in a 1 x n board. The cells are numbered from 0 to n-1, where the left most cell is marked as cell 0. Each cell can contain at most one piece.
There are two kinds of pieces, gray and white. Alice moves all the gray pieces, and bob moves all the white ones. The pieces alternate, that is, leftmost piece is gray, next is white, next to that is gray, then it's white again, and so on. There will always be equal number of black and gray pieces. Alice can only move pieces to the right. Bob can only move pieces to the left.
In each move, a player selects one piece and moves that piece, either to its left (Bob) or to its right (Alice), any number of cells (at least 1) but, it can neither jump over other pieces, nor it can move outside of the board. The players alternate their turns.
For example, if Alice decides to move the left most gray piece, these two moves are available to her.
| Illustration | |
|---|---|
| Fig 1: Initial Position |  |
| Fig 2: Alice moving the gray piece one cell to the right |  |
| Fig 3: Alice moving the gray piece two cells to the right |  |
Alice moves first. The game ends, when someone is unable to make any move, and loses the game. You can assume that, both of them play optimally (that is, if it is possible to apply a strategy that will ensure someone's win, he/she will always use that strategy).
Now you are given a configuration of a board, you have to find the winner.
Input
Input starts with an integer T (≤ 200), denoting the number of test cases.
Each case starts with a line containing an integer k (1 ≤ k ≤ 100) denoting the number of gray pieces in the board. The next line contains 2k distinct integers (in ascending order) denoting the position of the pieces. The first integer denotes a gray piece, the second integer denotes a white piece, the next integer denotes a gray piece and so on. All the integers will lie in the range [0, 109].
Assume that n is sufficiently large to contain all the pieces. And at least one move is remaining.
Output
For each case, print the case number and Alice or Bob depending on the winner of the game.
Sample
| Sample Input | Sample Output |
|---|---|
2 2 0 3 7 9 2 1 3 7 9 | Case 1: Alice Case 2: Bob |

 So having a clear concept of the topic mentioned above, we can solve this problem.
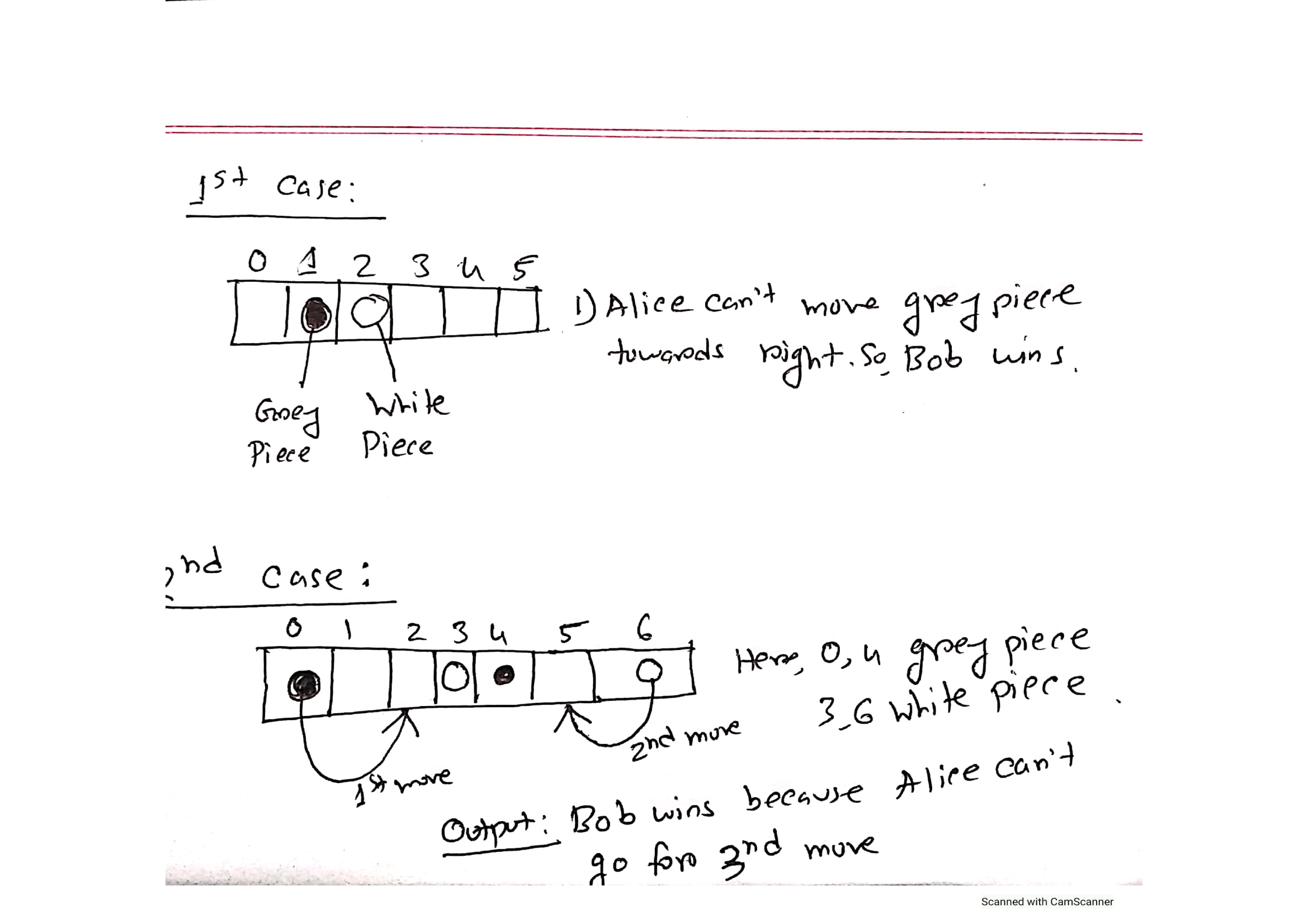
Now for the sake of making the explanation easier consider me as Alice and you are Bob.Now let's think that I have a piece at position 2 and you have a piece at 3 and there are no additional pieces.
Since I am allowed to move towards the right only,I can't move as there are no empty cells towards right and since my movement is zero for a move,I lost.So we can say,zero is a losing state and I,as the first player failed to give a non-zero state to the opponent which if my opponent failed to make a zero state and return to me,he would have lost.
The winner of the game always tries to make xor zero with the change brought by the loser of the game.In this case,I failed at giving you a non zero state which is why I lost.
Now,let's play a game to simulate the entire thing for a better understanding.
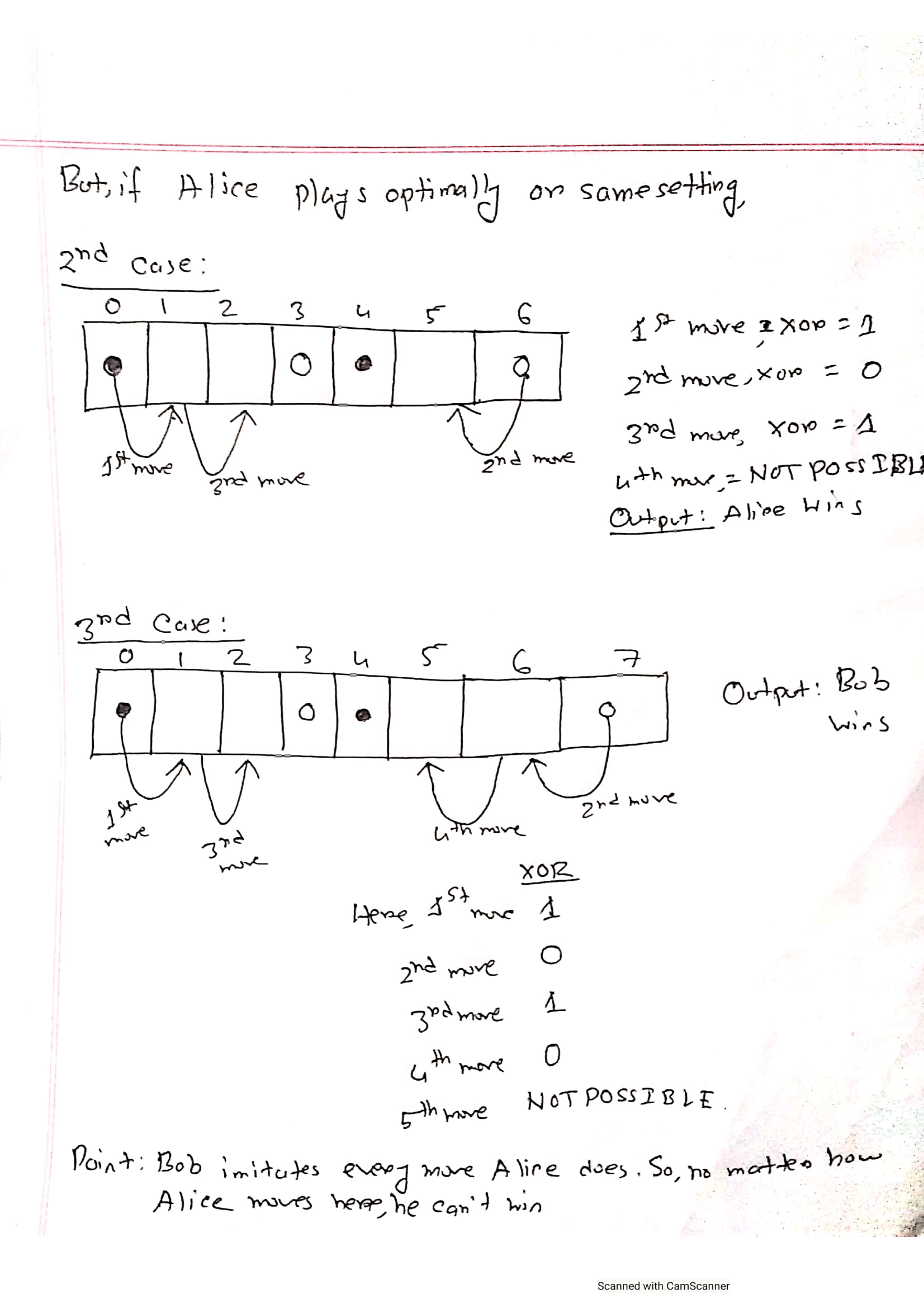
Suppose I have 2 pieces at 0 and 7 and you have 2 pieces at 3 and 9.
Since I am going for the first move,I have two options for first move.
1)Either,I move one step of my first piece to the right and set it to position 1,or.
2)I can move two step of my first piece to the right and set it to position 2.
But I can't move 3 steps to the right because you have your first piece there and the rule of the game is I am not allowed go over your piece.
So,now I went with the first option and now my xor is 1,I gave you a nonzero state to you and now my first piece is at 1. Now if you wish to defeat me,you will have to give me a zero state by mirroring my own move.So,you can move only give one move with your second piece that is you can move your piece from the 9th index to the 8th index because I have one of my pieces at 7 and you succeeded at mirroring my move.If I had no piece left to move I would have lost.But I won't lose. Why?Well,it's because my first piece can still once more towards right and make xor=1 because it was at position 1 and your piece is at position 3.And I gave you a nonzero state but you can't mimic my move this time since you have no cells left to move and that's why you lost the game.
In the end,if I succeeded at giving you a non zero state which you failed at giving me a zero state,I win and if you gave me a zero state which I failed at turning into a non zero state, I lose.Now if you know how XOR works,you should be able to think how to implement this.
So having a clear concept of the topic mentioned above, we can solve this problem.
Now for the sake of making the explanation easier consider me as Alice and you are Bob.Now let's think that I have a piece at position 2 and you have a piece at 3 and there are no additional pieces.
Since I am allowed to move towards the right only,I can't move as there are no empty cells towards right and since my movement is zero for a move,I lost.So we can say,zero is a losing state and I,as the first player failed to give a non-zero state to the opponent which if my opponent failed to make a zero state and return to me,he would have lost.
The winner of the game always tries to make xor zero with the change brought by the loser of the game.In this case,I failed at giving you a non zero state which is why I lost.
Now,let's play a game to simulate the entire thing for a better understanding.
Suppose I have 2 pieces at 0 and 7 and you have 2 pieces at 3 and 9.
Since I am going for the first move,I have two options for first move.
1)Either,I move one step of my first piece to the right and set it to position 1,or.
2)I can move two step of my first piece to the right and set it to position 2.
But I can't move 3 steps to the right because you have your first piece there and the rule of the game is I am not allowed go over your piece.
So,now I went with the first option and now my xor is 1,I gave you a nonzero state to you and now my first piece is at 1. Now if you wish to defeat me,you will have to give me a zero state by mirroring my own move.So,you can move only give one move with your second piece that is you can move your piece from the 9th index to the 8th index because I have one of my pieces at 7 and you succeeded at mirroring my move.If I had no piece left to move I would have lost.But I won't lose. Why?Well,it's because my first piece can still once more towards right and make xor=1 because it was at position 1 and your piece is at position 3.And I gave you a nonzero state but you can't mimic my move this time since you have no cells left to move and that's why you lost the game.
In the end,if I succeeded at giving you a non zero state which you failed at giving me a zero state,I win and if you gave me a zero state which I failed at turning into a non zero state, I lose.Now if you know how XOR works,you should be able to think how to implement this.