LightOJ 1375 - LCM Extreme
You are given T test cases, for each test case you are given n <= 3x106.
You have to find sum of LCM of all pairs (i, j) such that 1 <= i, j <= n.Here, lcm refers to the least common multiple of some integers, i.e. the smallest integer that is a multiple of all of the given integers (modulo 2^32).
Summary
To solve that problem we have to use the LCM Sum Formula. It looks like following:
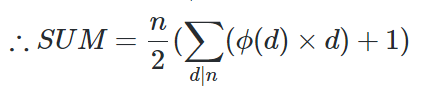
Where, SUM = lcm(1, n) + lcm(2, n) + lcm(3, n) + ... + lcm(n, n). It's pseudocode looks like following:
int lcm_sum_function(int n):
sum = 0
for d in divisor_of[n]:
sum += phi[d] * d
return (n * (sum + 1)) / 2
Here, phi[n] refers to the Euler Totient Function for n.
Recommended: SPOJ LCMSUM - LCM Sum
Solution
We will precalculate phi[n] beforehand for all possible n (till 3x106, that is).
Naive Approach
Let mx = 3e6+9. Since, for all possible n, we have to iterate over all the divisors of n, let's precalculate all the divisors of n using the following pseudocode:
vector <int> v
for i = 1; i < mx; i++:
for j = i; j < mx; j += i:
divisors_of[j].push_back(i)
Now, if we need to iterate over divisors of x, we can iterate over the element of divisors_of[x], which should save some time. For each x, calculating this might take logarithmic time.
Since we need to calculate the sum of the LCM Sum Function of all possible i till n, we can do the following:
ans = 0
for i = 1; i <= n; i++:
ans += lcm_sum_function(i)
return ans
Problem with Naive Solution
n can be equal to 3x106, and T can be equal to 2x105 . For each test case, we have to calculate lcm_sum_function(i), where it takes O(log2i), for all i till n. So, total complexity will be O(T n log2 n) , which won't pass the time limit of 3s.
Faster Approach
If we can precalculate res[i] = lcm_sum_function(i) for all possible i beforehand, and then we can apply prefix sum technique. After using prefix sum, res[i] would mean sum of lcm_sum_function for all j till i. Then we can output the result for each testcase in O(1) time.
The preprocessing needs O(n log2n) operations to complete, if we cleverly calculate for all n, lcm_sum_function(n) using the pseudocode of calculating divisors.
Applying prefix sum needs O(n) time.
So, total complexity for T cases = O(n + T + n log2n) , which passes the 3s time limit.
C++ code
#include "bits/stdc++.h"
using namespace std;
using ull = unsigned long long;
const int mx = 3e6 + 9;
int phi[mx];
ull res[mx];
bitset <mx> mark;
void sieve_phi() {
for (int i = 1; i < mx; i++) phi[i] = i;
mark[1] = 1;
for (int i = 2; i < mx; i++) {
if (mark[i]) continue;
for (int j = i; j < mx; j += i) {
mark[j] = 1;
phi[j] = phi[j] / i * (i - 1);
}
}
}
void calc() {
for (int i = 1; i < mx; i++) {
for (int j = i; j < mx; j += i) {
res[j] += (ull(i) * phi[i]);
}
res[i]++;
res[i] /= 2;
res[i] *= i;
res[i] -= i;
}
for (int i = 2; i < mx; i++) res[i] = res[i] + res[i - 1];
}
int main() {
sieve_phi();
calc();
int tc; scanf("%d", &tc);
int t = 0;
while (tc--) {
int n; scanf("%d", &n);
ull ans = res[n];
printf("Case %d: %llu\n", ++t, ans);
}
}
Tutorial source