LOJ 1211 - Intersection of Cubes

You are given n cubes, each cube is described by two points in 3D space: (x1, y1, z1) being one corner of the cube and (x2, y2, z2) being the opposite corner. Assume that the sides of each of the cubes are parallel to the axis. Your task is to find the volume of their intersection.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 100). Each of the next n lines contains six integers x1 y1 z1 x2 y2 z2 (1 ≤ x1, y1, z1, x2, y2, z2 ≤ 1000, x1 < x2, y1 < y2, z1 < z2) where (x1, y1, z1) is the co-ordinate of one corner and (x2, y2, z2) is the co-ordinate of the opposite corner.

Output

For each case, print the case number and volume of their intersection.

Solution

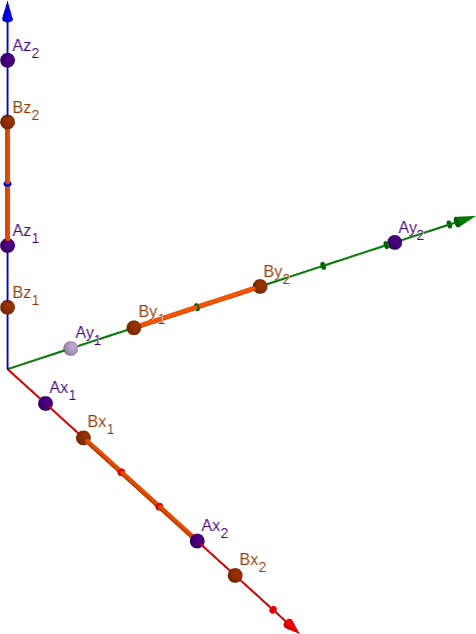
We know that the Volume of a Cube = Height * Width * Length. For any P -axis, we can find out length of the common part simply by, (p₂ which is near to origin point among all values of p₂) - (p₁ which is the most furthest from origin point among all values of p₁). More clearly, we need the highest possible value among the inputs for p1 and the lowest possible value among the inputs forp2 for any P-axis. And length of the common part here will be p₂ - p₁. Note that, we are not going to take the absolute value because there may be a scenario where there is no common part at all and in such case negative value for any single axis will indicate that it is impossible, or simply Volume = 0.

Example of a valid case : from the graph, in X-axis, Bx1 is the further from 0 than Ax1 & Ax2 is nearer to 0 than Bx2. Thus, common length in X-axis = Ax2 - Bx1.

Example of an impossible case : A = {(1,2),(2,5),(1,9)} and B = {(3,4),(2,5),(1,9)}. Here, xNear = 2 which belongs to A and xFar = 3 which belongs to B. Even A and B has the same length in every axis but xNear-xFar = -1. Thus we know that even though the cubes have same length in dimensions but no intersection.

When we have the common part from all the axis, multiplying them will give us the result, Area = (xNear-xFar)*(yNear-yFar)*(zNear-zFar). And in case of a negative common length for any axis, the result will be 0.

The above implementation is accepted.

Solution in C

#include <stdio.h>

int main()
{
    int t, n, x1, y1, z1, x2, y2, z2, xCommon, yCommon, zCommon;

    scanf("%d", &t);
    for (int i = 1; i <= t; i++)
    {
        int xFar = 0, yFar = 0, zFar = 0;
        int xNear = 1001, yNear = 1001, zNear = 1001;
        scanf("%d", &n);
        for (int j = 1; j <= n; j++)
        {
            scanf("%d %d %d %d %d %d", &x1, &y1, &z1, &x2, &y2, &z2);

            if (x1 > xFar)
                xFar = x1;

            if (y1 > yFar)
                yFar = y1;

            if (z1 > zFar)
                zFar = z1;

            if (x2 < xNear)
                xNear = x2;

            if (y2 < yNear)
                yNear = y2;

            if (z2 < zNear)
                zNear = z2;
        }
        xCommon = (xNear - xFar);
        yCommon = (yNear - yFar);
        zCommon = (zNear - zFar);

        if (xCommon > 0 && yCommon > 0 && zCommon > 0)
            printf("Case %d: %d\n", i, xCommon * yCommon * zCommon);
        else
            printf("Case %d: 0\n", i);
    }
    return 0;
}

Tutorial source