LOJ 1417 - Forwarding Emails

First of all, there are some people and you have to send them some mail. Now suppose you know that, if you send a mail to the 1st person, he will be able to forward the mail to the 2nd person. Here, one can send mail to another only when there is a connection between them. Suppose, there is connection between 1st person and 2nd person and there is connection between 2nd and 3rd person but there is no connection between 1st and 3rd person. If you want to send mail to 1st person to 3rd person, you have to send it through 2nd person. Now in this problem you have to find the first person so that, you may send mail to maximum number of people. We may try to understand the problem through an example.

Example: 1 2 - 1st person can send mail to 2nd person 2 1 - 2nd person can send mail to 1st person 5 3 - 5th person can send mail to 3rd person 3 4 - 3rd person can send mail to 4th person 4 5 - 4th person can send mail to 5th person

Here the graph is:

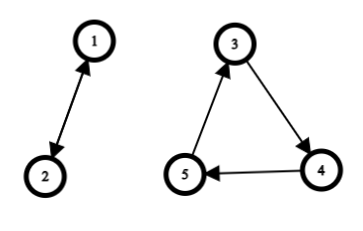
So here, if I send mail to the 1st person first, then he can only send the 2nd person, then the mail will reach to 2 people in total. If I send mail to the 2nd person first, then he can only send the 1st person, then the mail will reach to 2 people in total. If I send mail to the 3rd person first, then he can only send the 4th and 5th person, then the mail will reach to 3 people in total. Similarly, even if the mail is sent to the 4th and 5th people first, the mail will reach to 3 people in total.

That means I can send mail to maximum three people when I send mail 3rd, 4th or 5th person first. Since we have to print the minimum value or person who can send mail to the maximum people so the answer is 3.

Here the answer is only if we can find out all the maximum connected groups. Then 1,2 will be in the same group and 3,4,5 will be in another group, which can be easily implemented by using BFS or DFS algorithm.

If we run a loop from the first and run a DFS from the 1st person, we can visit 1,2, then we don't need to run the DFS from the 2nd person anymore, In the same way, if we run a DFS with 3rd person, we can visit 3,4,5, then we don't need to run DFS from 4th, 5th person. So, DFS will run 2 times, from 1st and 3rd person. Since the maximum number of people can be mailed by 3rd person, then the last answer is 3rd.

If you are still stuck with this problem, check the codes below:

C++

#include<bits/stdc++.h>
using namespace std;
int vis[50005],dist[50005],adjacent[50005],cnt=0;
int dfs(int uu)
{
    vis[uu]=1;
    int vv=adjacent[uu];
    if(!vis[vv])
    {
        cnt++;
        dfs(vv);
    }
    vis[uu]=0;
    return dist[uu]=cnt;

}
main()
{   
    int ts,cs=1;
    scanf("%d",&ts);
    while(ts--)
    {
        int n,u,v,mx=0,ans=0;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d",&u,&v);
            adjacent[u]=v;
        }
        memset(vis,0,sizeof(vis));
        memset(dist,-1,sizeof(dist));
        for(int i=1;i<=n; i++)
        {
            cnt=1;
            if(dist[i]==-1)
            {
                dfs(i);
                dist[i]=cnt;
            }
            if(cnt>mx)
            {
                mx=cnt;
                ans=i;
            }
        }

        printf("Case %d: %d\n",cs++,ans);
    }
}

Tutorial source