LightOJ 1054 - Efficient Pseudo Code
Summary
You'll be given two integers, n and m. You have to print the sum of all divisors of nm, modulo 1000000007.
Hint
I highly recommend trying the problem LightOJ 1336 - Sigma Function, or at the very least, read the statement carefully before trying this problem.
If you read that problem, you'll come to know about this formula:
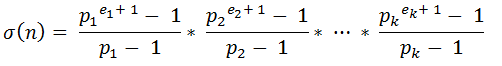
where σ(n) is the sum of divisors of n.
From this formula, we can see that we only need the Prime factors of nm and how many times each prime factors appear. This seems a little difficult task since nm can be a huge number. Let's see how we can solve this part of the problem.
Let's factorize 6. The primes are 2, 3.
Now factorize 62 = 36. The primes are 2, 2, 3, 3.
How about 63 = 216?
The primes are 2, 2, 2, 3, 3, 3.
Did you notice any pattern?
Yes, the count of primes are multiplied. If you think and observe a little, you'll find out that nm will have all the prime factors of n, no extra primes, and each primes factor will appear m times more than it appeared in n.
So now all you have to do is to factorize n, count the frequency of prime factors, then multiply each factors frequency by m.
Now you can solve this problem using the formula given before.
You'll also need Bigmod and Modular Inverse to solve this problem. If you don't know what they are, check these links:
Modular Addition and Subtraction
Modular Arithmetic
Modular Inverse
You may also need to know about the Fermat's Little Theorem if you try to understand modular inverse.
Code
Please try your best to solve the problem on your own before watching the source code.
C++
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL mod = 1000000007;
vector<LL> primes;
map<LL, LL> times;
LL bigmod (LL b, LL p, LL m)
{
if (p==0) return 1;
if (p%2==0) {
LL x=bigmod(b, p/2, m)%m;
return (x*x)%m;
}
else return (b%m * bigmod(b, p-1, m))%m;
}
LL inv_mod(LL a, LL m) {
return bigmod(a, m-2, m);
}
void factorization(long long n) {
if (n % 2 == 0) {
primes.push_back(2);
while (n % 2 == 0) {
times[2]++;
n /= 2;
}
}
for (long long d = 3; d * d <= n; d += 2) {
if (n % d == 0) {
primes.push_back(d);
while (n % d == 0) {
times[d]++;
n /= d;
}
}
}
if (n > 1) {
if (!times[n])
primes.push_back(n);
times[n]++;
}
}
int main()
{
int t, ca=1;
cin>>t;
while (t--) {
primes.clear();
times.clear();
LL n, m;
cin>>n>>m;
factorization(n);
for (auto i: primes) {
times[i] *= m;
}
LL ans = 1;
for (auto i: primes) {
LL now = bigmod(i, times[i] + 1, mod);
now -= 1;
if (now < 0)
now += mod;
LL low = inv_mod(i - 1, mod);
now *= low;
ans = ((ans % mod) * (now % mod)) % mod;
}
cout<<"Case "<<ca++<<": "<<ans<<endl;
}
return 0;
}
If you have trouble understanding the condition if (now < 0) at line 69 and 70 of the code, you can check this blog.
Happy Coding ^_^
Tutorial source