LOJ 1040 - Donation

Problem Summary

Your house has n rooms and they are possibly connected with ethernet cables of different lengths. You want to keep some cable for the house and donate the rest of the cables. Your target is to maximize donation length so you will use the least possible length of the cables to keep the rooms connected.

And if all the rooms are not connected through some cable path even before donation, print -1.

Observations

We can see the following properties in the problem structure.

• Graph: We can consider the rooms of the house as nodes in a graph, and the cables as edges. Since the lengths of cables are given, and the connections have no direction, this is a Weighted Undirected Graph.

• Tree: We have to remove some cables or edges for donation. To remove the most possible edges, we can reduce the graph into a tree. Tree uses N-1 edges to connect N nodes, and removing any more edge is not possible since this will disconnect the network.

• Minimum Spanning Tree: We want to maximize the length of cables donated. So we have to use the least possible cable length to construct the tree. So, the problem is actually about converting the graph into a Minimum Spanning Tree.

  • Minimum Spanning Tree of a graph is a subtree of that graph that contains all the nodes and the sum of edge weights is minimum possible. You can use Prim's algorithm or Kruskal's Algorithm to implement the Minimum Spanning Tree.

Solution

In our approach, we will use DFS to check for connectivity and Kruskal's Algorithm to compute MST. If you already got an idea by reading thus far, try to code yourself first without reading further.

The input will be given as a 2D list, where the i, j index will denote the length of cable that connects room i to room j.

• We will only push edge information to the graph when the edge weight is bigger than zero, to avoid redundancy and extra check for zero edges.

• We will keep the sum of all the cable lengths in a variable totalLength.

• We will create an Adjacency List and an Edge List from the given input.

• First, we have to check if the graph is connected. We will run a DFS from any node once and check if it visits all n nodes in one go. Adjacency List can be used to run dfs. If it does not visit all n nodes, then the graph is disconnected. In that case, print -1.

• If the graph is connected, then we will compute the Minimum Spanning Tree of the graph. We can apply Kruskal's Algorithm with the Disjoint-Set Union method on the Edge List.

• Then the answer will be totalLength - mst, where mst being the sum of all edge weights (cable lengths) in the Minimum Spanning Tree. This is the most amount of cable length we can donate.

Simulation

Simulation of test case 2

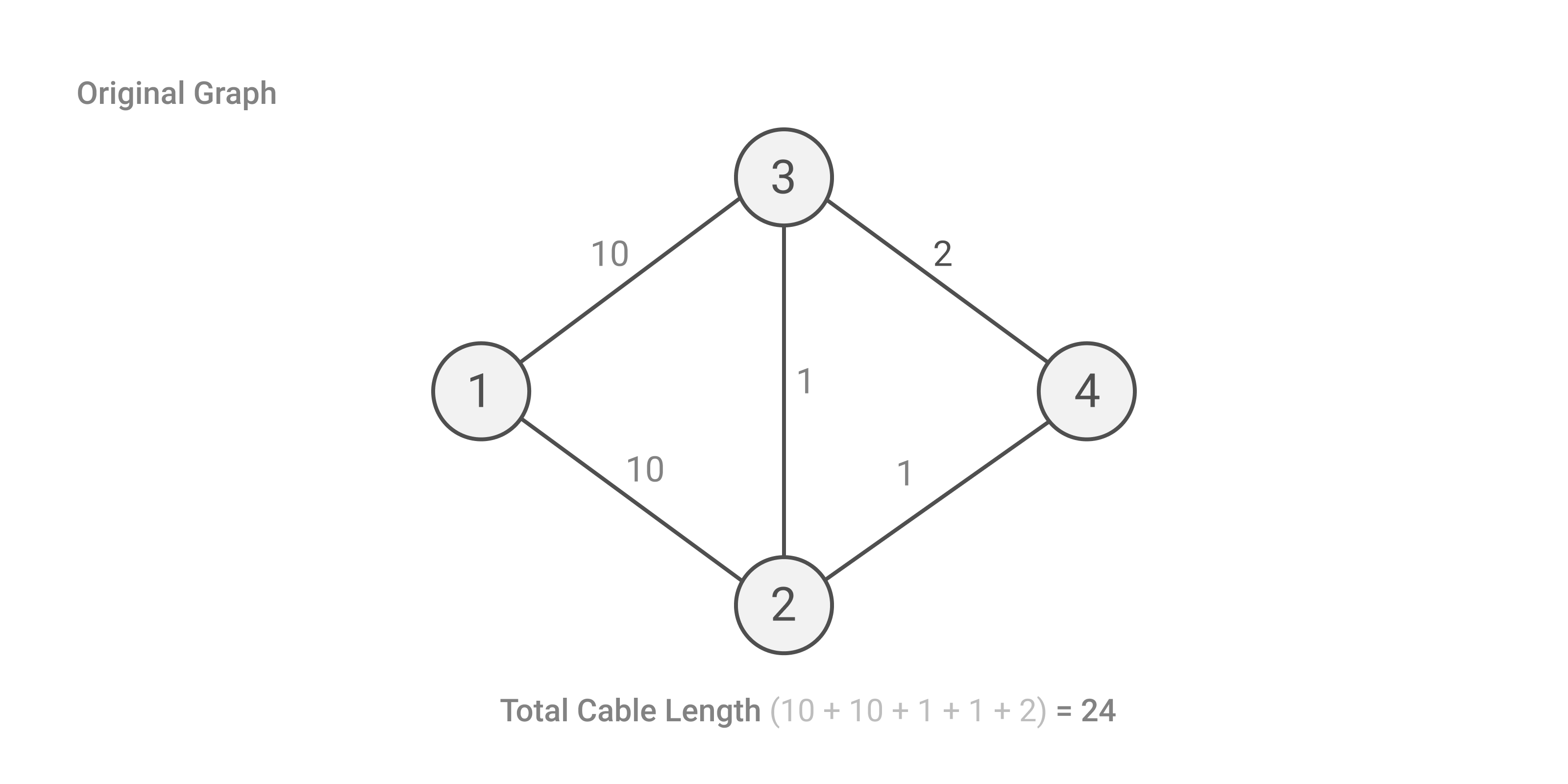
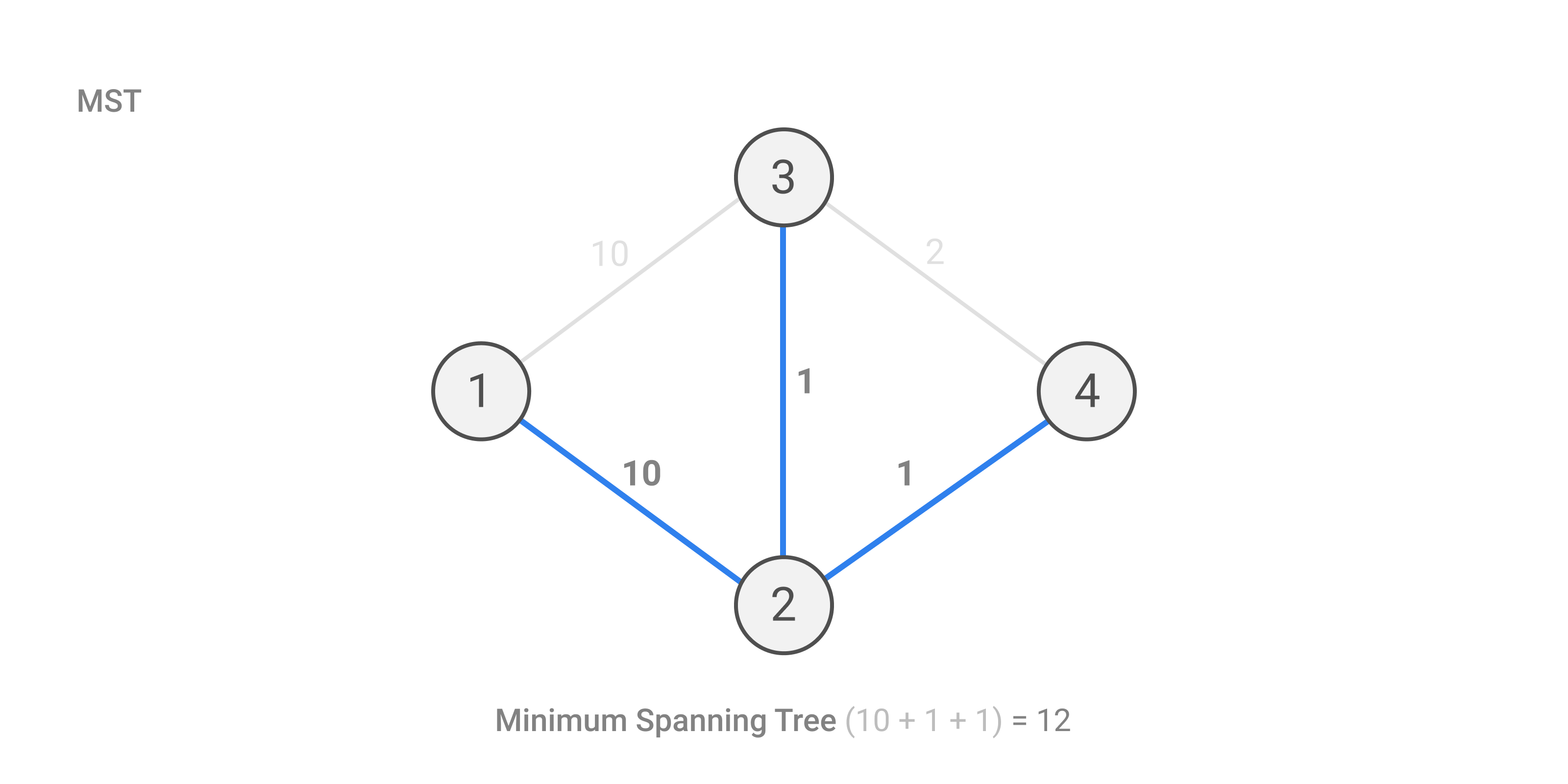
And the answer is totalLength - mst. Since 24 is the total cable length and the minimum cable length necessary to connect all rooms is 12. Answer = 24 - 12 = 12.

Simulation of test case 3

We print -1 since the graph is not connected.

C++

#include<bits/stdc++.h>
using namespace std;
#define MAX 55

struct edge{
    int u, v, w;
};

vector <edge> G; // Edge List (used in Kruskal's)
vector <int> graph[MAX]; // Adjacency List (Used in DFS)

bool cmp( edge A, edge B ){
    return A.w < B.w;
}

int parent[MAX];
bool vis[MAX];
int n; // total nodes
int cnt; // counter variable to check how many nodes are visited in dfs

// reset data structures for every test case
void reset(){
    G.clear();
    for (int i = 0; i < MAX; i++){
        parent[i] = i;
        graph[i].clear();
        vis[i] = 0;
    }
    cnt = 0;
}

// dfs function to traverse the graph
void dfs(int n){
    vis[n] = 1;
    cnt++; // increment counter as we visit a node
    for (int i = 0; i < graph[n].size(); i++){
        int v = graph[n][i];
        if (!vis[v])
            dfs(v);
    }
}

// find parent of a disjoint-set
// used in MST
int Find(int u){
    if (u == parent[u]) return u;
    return parent[u] = Find(parent[u]);
}

// compute MST cost
// Uses Kruskal's Algorithm with Disjoint-Set Union method
int MST (){
    int cost = 0;
    sort(G.begin(), G.end(), cmp);

    for (int i = 0; i < G.size(); i++){
        int u = G[i].u;
        int v = G[i].v;
        int w = G[i].w;

        int p = Find(u);
        int q = Find(v);
        if (p!=q){
            parent[q] = p;
            cost += w;
        }
    }

    return cost;
}

// function to check if every node is reachable from any other
bool check(int node){
    dfs(node);
    return cnt == n;
}


int main()
{
    int T; scanf("%d", &T);
    for (int cs = 1; cs <= T; cs++){
        reset(); // reset all data structures

        scanf("%d", &n);

        int totalLength = 0; // sum of all cable lengths
        for (int i = 1; i <= n; i++){
            for (int j = 1; j <= n; j++){
                int w; scanf("%d", &w);
                if (w){ // if weight is non-zero
                    // insert into edge list
                    G.push_back({i, j, w});
                    // insert into adjacency list
                    graph[i].push_back(j);
                    graph[j].push_back(i);
                }
                totalLength += w; // update total length
            }
        }

        // if the graph is not connected, print "-1"
        // we run dfs from node 1, any node can be used
        if (!check(1)){
            printf("Case %d: -1\n", cs);
            continue;
        }

        int mst = MST();
        int answer = totalLength - mst;
        printf("Case %d: %d\n", cs, answer);
    }

    return 0;
}

Tutorial source