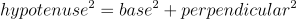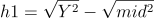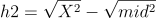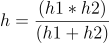1062 - Crossed Ladders :

A ladder with length X rested from the base and lean with the right building. Another ladder with length Y rested from another right side's base and lean with the left side's base. These two ladders are crossed at a point N. The length between M and N is h. We have to find the width d of the road.

In this problem, you are given T testcases to execute. For each test case you will be given X, Y and h. You have to find the value of d for every single test cases.

Tutorial :

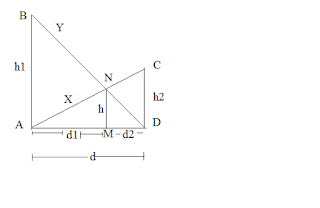
In the crossed ladder problem two ladder AC and BD crossed each other at point N. The length of AC and BD is X and Y respectively. You are also given the value of length h. Let's denote AB = h1 , CD = h2, AD = d . From these values, we can find out the value of d. Using basic observation it is pretty clear that the value of d will always be less than the values of X and Y. You can apply a bisection over this d length to get a nearly correct result.

From the theory of crossed ladder problem we can say that ,

See the images below for further clarifications about the equation.

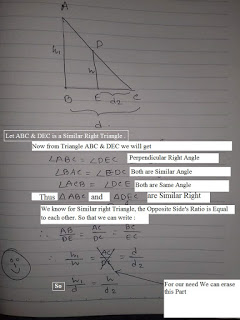
Hence We have the proof about the equation.

Now, we can start the bisection by denoting the parameters low = d = 0 and high = d = minimum(X, Y). Every time we have to find the mid value between low and high. A nice property that lies in the crossed ladder problem is when the width d increases the height h decreases and vice versa. That means from several mid values of width we just have found such a value that will fairly equal to h.

Let the mid = K ( in general d ) and you have the value of X. From pythagorean theorem, we know,

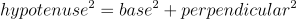
From this equation, We can show that -

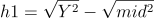
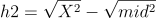
So, now you have the value of h1 and h2 . You can easily find ,

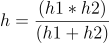
For a value of mid, we will found the approximate value of real h. Now for every calculated h, you easily can compare with the original h.

Code

#include<bits/stdc++.h>
#define DIST(x1,x2, y1, y2) (((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2)))
#define CLR(a) a.clear()
#define VCLR(a, n) for(int i=0; i<=n+3; i++) a[i].clear()
#define SIZE(a) a.size()
#define ERASE(a, b) memset(a, b, sizeof a)
#define PB(a, b) a.push_back(b)
#define PB2(a,i,b) a[i].push_back(b)
#define LL long long
#define DBG cout<<"I Am Here"<<endl
#define DBGA(a) cout<<a<<endl
#define DBGI(b,a) cout<<b<<' '<<a<<endl
#define DBGL(i,s,e,b) or(int i=s; i<=e; i++) cout<<b<<endl
#define INF 1e9
#define INV 1e-6
#define sl(a) scanf("%I64d", &a)
#define pl(a) printf("%I64d\n", a)
#define si(a) scanf("%d", &a)
#define pii pair<int,int>
#define MAX 600005
#define CASE(i) printf("Case %d: ", i);
#define PI acos(-1)
#define EPS 0.00000001

using namespace std;

double x, y, c;

double solve(double mid)
{
    double A = sqrt((x*x) - (mid*mid));
    double B = sqrt((y*y) - (mid*mid));

    //cout<<A<<' '<<B<<endl;
    return ((A*B)/(A+B));
}

int main()
{
    int test;
    scanf("%d", &test);
    for(int caseno = 1; caseno<=test; caseno++)
    {
        scanf("%lf %lf %lf", &x, &y, &c);
        double lo = 0.0, hi = min(x, y), mid;

        int cnt = 100;
        double ans = 1;
        while(cnt--)
        {
            mid = (lo + hi)/2.0;
            //cout<<solve(mid)<<endl;
            if(solve(mid)<=c)
            {
                hi = mid;
            }
            else
            {
                lo = mid;
            }
        }
        printf("Case %d: %0.10lf\n", caseno, lo);
    }
}

Tutorial source