LOJ 1002 - Country Roads

Tags : graph, single source shortest path

We will be given information of an area map (undirected graph / bi-directional graph) through the number of cities (nodes),number of roads (edges) in total and the cost (weight) for each pair of linked cities via the road. And we will also be given t the home town (the staring node) and we have to print out the minimum cost to reach this town from other cities.

Helpful Resources

• Graph (abstract data type) - Wikipedia

• Dijkstra's algorithm - Wikipedia

• Dijkstra’s shortest path algorithm - GeeksForGeeks

• Explanation of Dijsktra (Video)

Solution

At first we will simply create a graph structure for the Area Map in any preferred method (adj. matrix/ linked list). The problem statement has confirmed : (1) there shall be no negative cost for the roads and (2) the graph is a bi-directional/undirected graph. We can apply Dijsktra's Algorihtm or its derivative or any similar. But we must keep in mind that we are finding many dedicated optimal paths(one path per one city), not one optimal path to traverse all the cities in 1 go. For each individual city's optimal path, we take the minimum from all the path's costs. Here, a path's cost = maximum weighted road encountered which we will be saving in a separate array/list.

We at first update the cost if the two cities have directly connected edges among them, and in that case we will only keep the lowest possible weight. It's a duplicate we get rid off while taking inputs for edges. Let's look at the Case 2's inputs':

5 4
0 1 5
0 1 4
2 1 3
3 4 7
1

In this case, 0 1 5 and 0 1 4 are inputs for 0 -- 1 edge along with the weight/cost. We will update while taking inputs and update from cost[0,1] = 5 to cost[0,1] = 4 as it is minimum among those two directly connected edges.

Now we need to traverse and update costs. We will take another graph example to discuss how we are traversing. We will go full brute force by not leaving any route for a home town to another city untried. For example:

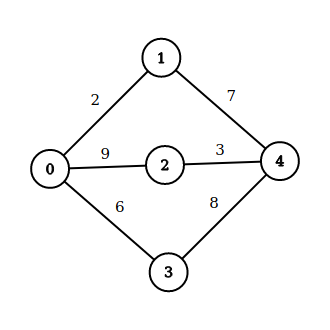
All the possible paths for 1 to 2:

This is how we are traversing, leaving no path untried. We just update the distance array/list for [1,2] = 7 as it is the minimum. We are only updating the cost of the destination. We repeat this process for from home town to all the other cities and ultimately get the distance array/list.

What would happen if we had marked to avoid repetition so that we find just one single optimal path to travel them all in 1 go?

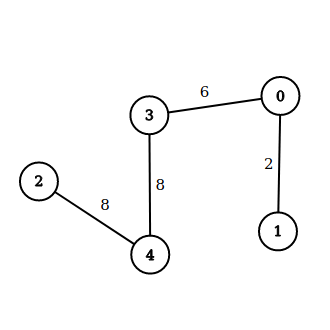
We have constructed a single optimal path, but the only thing wrong here is [1,2] = 8 which is the wrong answer. Thus we are not to use any algorithm that re-maps the whole area or does not check all possible routes in a brute force manner.

Caution : Remember to use fast I/O for your preferred language as per the suggestion from the problem statement and find out what may disrupt them to avoid it.

The above implementation is accepted.

Solution in C++

#include <bits/stdc++.h>
using namespace std;

int main()
{
    //Enabling fast I/O for Cpp. Don't use anything that disrupts fast I/O (For example: `endl`).
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int testCases, numberOfCities, numberOfRoads,
        sourceCity, destinationCity, roadCost, homeTown, maxCostFound;
    /*
    sourceCity = edge's first endpoint
    destinationCity = edge's second endpoint
    homeTown = source node from where we traverse

    */

    cin >> testCases;

    for (int i = 1; i <= testCases; i++)
    {
        cin >> numberOfCities >> numberOfRoads;

        vector<int> areaMap[numberOfCities];      //actual graph
        int distanceFromHomeTown[numberOfCities]; //distance output array
        int cost[numberOfCities][numberOfCities]; //road costs

        memset(cost, 0, sizeof(cost)); //initially setting the costs as not specified
        for (int i = 0; i <= numberOfCities; i++)
            distanceFromHomeTown[i] = INT_MAX;

        //Adding each given roads while checking if already a low cost road exist between them or not
        for (int i = 0; i < numberOfRoads; i++)
        {
            cin >> sourceCity >> destinationCity >> roadCost;

            if (cost[sourceCity][destinationCity]) //checking any previous road exists or not
            {
                cost[sourceCity][destinationCity] = cost[destinationCity][sourceCity] = min(cost[sourceCity][destinationCity], roadCost);
            }
            else
            {
                //adding new road
                areaMap[sourceCity].push_back(destinationCity);
                areaMap[destinationCity].push_back(sourceCity);
                cost[sourceCity][destinationCity] = cost[destinationCity][sourceCity] = roadCost;
            }
        }

        cin >> homeTown;

        queue<int> cityQueue; //making a queue to traverse through each of the city

        cityQueue.push(homeTown); //pushing the home town as our start point or source node

        distanceFromHomeTown[homeTown] = 0;

        while (!cityQueue.empty())
        {


            int startingCity = cityQueue.front();

            cityQueue.pop(); //taking it out since it will be traversed now

            //Checking the other cities that can be reached via startingCity

            /*
            don't sum previous road costs along the way and update.  
            as per problem requirement, we only update the `distance array` by `maximum weight` encountered, not the `cost` array.
            don't check for duplicate enqueue as we may find a better path that has lesser max value.
            we need to go full brute force leaving no path unchecked because of the problem requirements.
            */

            for (int i = 0; i < areaMap[startingCity].size(); i++)
            {
                int currentCity = areaMap[startingCity][i];
                maxCostFound = max(distanceFromHomeTown[startingCity],
                                   cost[startingCity][currentCity]);
                if (distanceFromHomeTown[currentCity] > maxCostFound)
                {
                    distanceFromHomeTown[currentCity] = maxCostFound;
                    cityQueue.push(currentCity);
                }
            }
        }

        cout << "Case " << i << ":\n";
        for (int i = 0; i < numberOfCities; i++)
            if (distanceFromHomeTown[i] == INT_MAX)
                cout << "Impossible\n";
            else
                cout << distanceFromHomeTown[i] << "\n";
    }

    return 0;
}

Tutorial source