LOJ 1029 - Civil and Evil Engineer

Problem Summary

You have n houses [1-n] and a power station 0. You are also given a set of wires, where every wire is in u v w format, meaning connection from u to v costs w. You have to use exactly n wires from the set to connect the houses with the power station. The connections can be direct or indirect (through some houses) but there must be a path of wires from every house to the power station.

Observations

We can see the following properties in the problem structure.

• Graph: We can consider the houses and the power station as nodes in a graph, and the wires as edges. Since the costs of connecting two nodes are given, and the connections have no direction, so this is a Weighted Undirected Graph.

• Tree: In total, we have n+1 nodes (n houses and 1 power station). We have to connect them using exactly n wires or edges. We know in a tree, for N nodes we have N-1 edges. So the problem is asking us to convert the graph into a tree.

• Minimum Spanning Tree: For the best possible connection scheme, We have to connect all houses with the power station using minimum cost. We have to pick edges in a way that satisfies the cost minimization. Therefore, we have to compute the Minimum Spanning Tree of the graph.

  • Minimum Spanning Tree of a graph is a subtree of that graph that contains all the nodes and the sum of edge weights is minimum possible. You can use Prim's algorithm or Kruskal's Algorithm to implement the Minimum Spanning Tree.

• Maximum Spanning Tree: We also have to calculate the maximum possible cost to connect all the nodes, since this is the worst possible connection scheme. For this, we have to pick edges in a way that maximizes the cost. So we also have to compute the Maximum Spanning Tree of the graph.

  • Maximum Spanning Tree of a graph is a subtree of that graph that contains all the nodes and the sum of edge weights is maximum possible. We can tweak the Minimum Spanning Tree algorithm (sort the edges in descending order of the weights) to implement Maximum Spanning Tree.

Solution

For every case, we have to calculate minimum spanning tree cost1 and maximum spanning tree cost2 and then average their costs, thus (cost1 + cost2) / 2. If (cost1 + cost2) is not divisible by 2 then we have to print in p/q format. Where p is (cost1 + cost2) and q is 2. For example, 229/2.

Simulation

Simulation of test case 2 is given below.

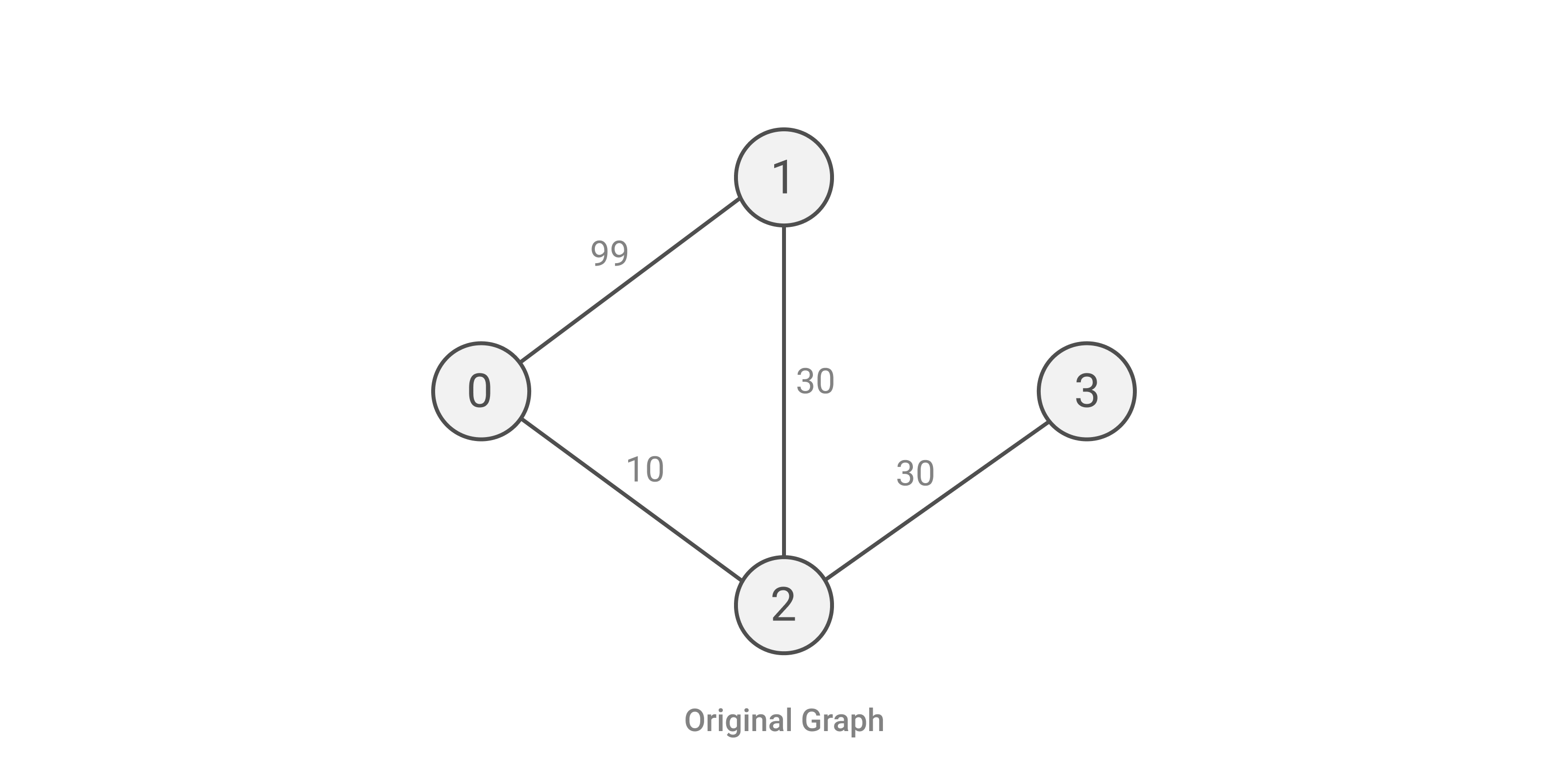
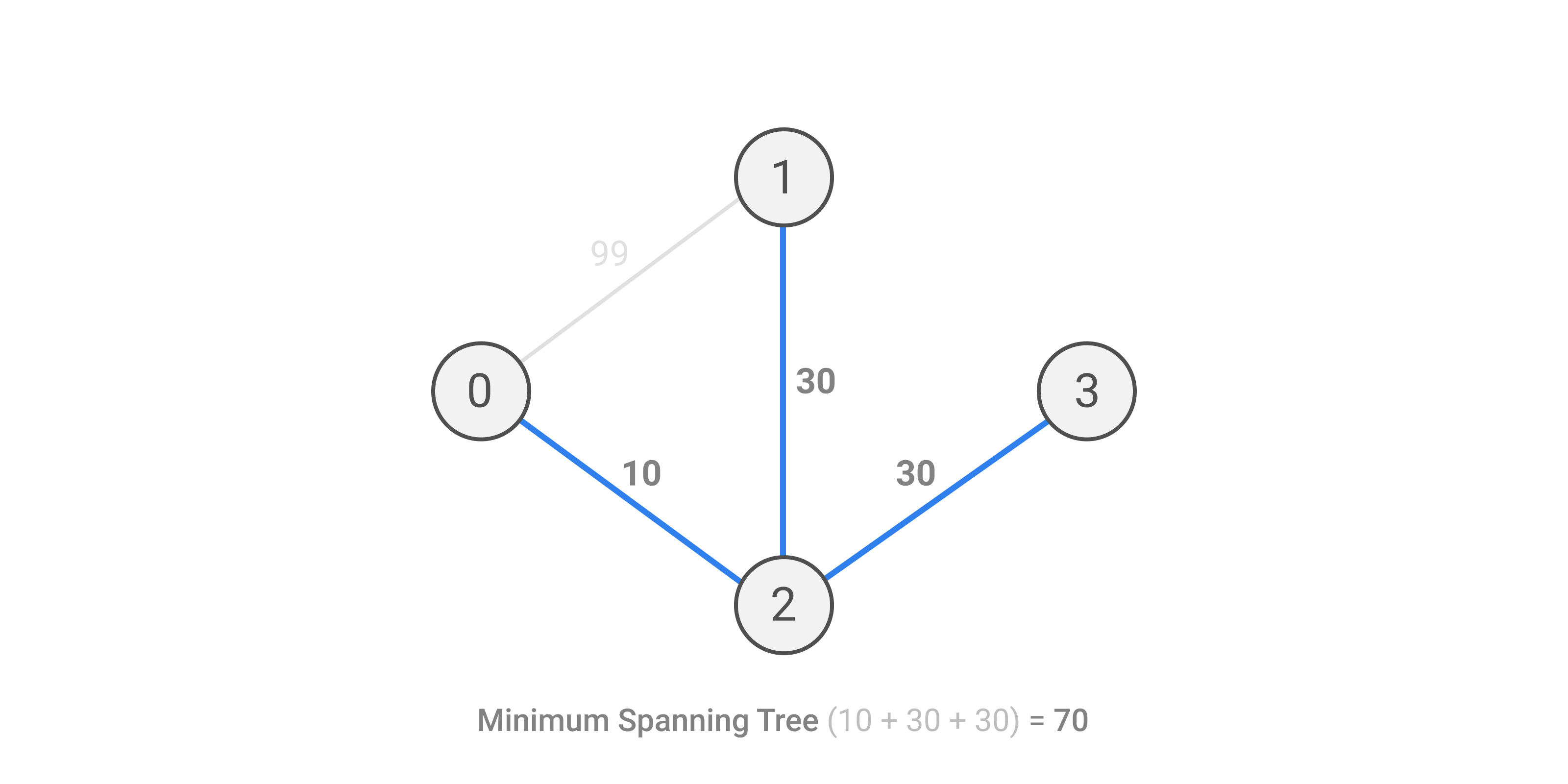
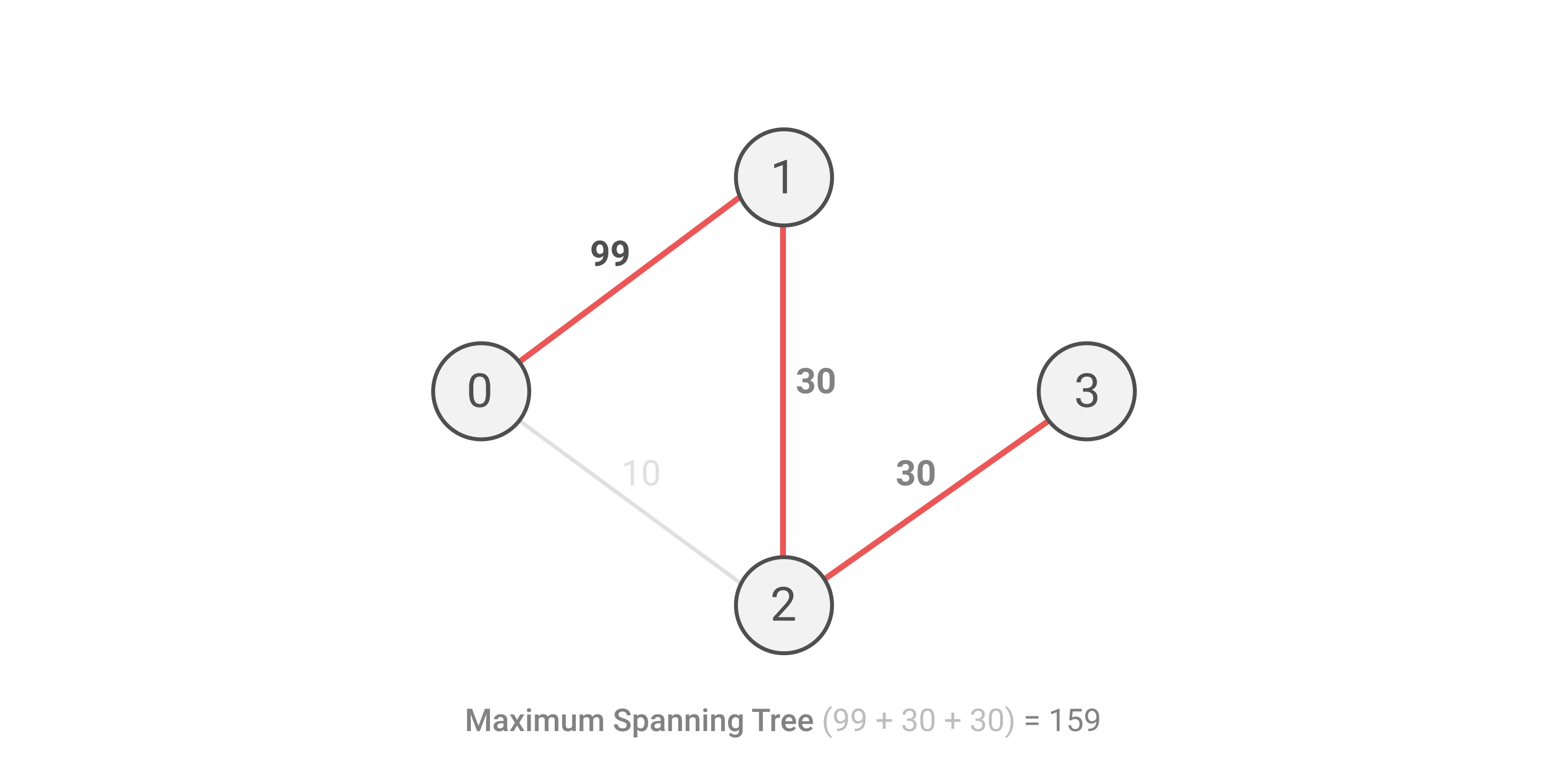
And the answer is (70 + 159) / 2. Since 229 is not divisible by 2, we print 229/2.

C++

#include<bits/stdc++.h>
using namespace std;

struct edge{
    int u, v, w;
};

bool cmp(edge A, edge B){
    return A.w < B.w;
}

// edge list
vector < edge > G;

int n; // total nodes
int parent[105];

// function to clear graph
void _init(){
    G.clear();
}

// function to find parent of a disjoint set
int Find(int u){
    if (u==parent[u]) return u;
    return parent[u] = Find(parent[u]);
}

// Kruskal's algorithm with Disjoint-Set Union method is used
// minimum spanning tree
long long MinST(){
    // reset parent table [0-n]
    for (int i = 0; i <= n; i++)
        parent[i] = i;

    long long cost = 0;
    // forward iteration for minimum cost first
    for (int i = 0; i < G.size(); i++){
        int u = G[i].u;
        int v = G[i].v;
        int w = G[i].w;

        int p = Find(u);
        int q = Find(v);
        if (p!=q){
            cost += w;
            parent[q] = p;
        }
    }
    return cost;
}

// maximum spanning tree
long long MaxST(){
     // reset parent table [0-n]
    for (int i = 0; i <= n; i++)
        parent[i] = i;

    long long cost = 0;
    // backward iteration for maximum cost first
    for (int i = G.size()-1; i >= 0; i--){
        int u = G[i].u;
        int v = G[i].v;
        int w = G[i].w;

        int p = Find(u);
        int q = Find(v);
        if (p!=q){
            cost += w;
            parent[q] = p;
        }
    }
    return cost;
}

int main()
{
    int T; scanf("%d", &T);
    for (int cs = 1; cs <= T; cs++){
        _init(); // reset graph

        scanf("%d", &n);
        int u, v, w;

        // take input until all u, v, w are zero (0)
        while ( scanf("%d%d%d", &u, &v, &w) && (u!=0 || v!=0 || w!=0) ){
            G.push_back({u, v, w});
        }

        // sorting is only done once
        // forward and backward iterations will be done
        // for ascending and descending order traversal
        sort(G.begin(), G.end(), cmp);

        long long cost1 = MinST();
        long long cost2 = MaxST();

        long long cost = cost1 + cost2;
        if (cost%2 == 0) printf("Case %d: %lld\n", cs, cost/2);
        else printf("Case %d: %lld/2\n", cs, cost); // cost/2 format
    }
    return 0;
}

Tutorial source