LOJ 1018 - Brush (IV)
What the problem wants
N number of 2D points are given. You have to find minimun number of straight lines that cover all the points.
Explanation with Example
Suppose for the input
1
7
10 10
11 11
12 12
12 13
11 13
10 14
9 15
The picture looks something like this.

Lets make saveral lines that covers all the points. For this we connect straight lines between (9, 15) and (10, 10); (10, 14) and (11, 11); (11, 13) and (12, 13); (12, 13) and (12, 12).
Then the picture seems something like this.

In this solution, we need 4 lines to cover all points.
After a bit of trying, we can see that we need at least 3 straight lines to cover all the points. The one result may seem like this.
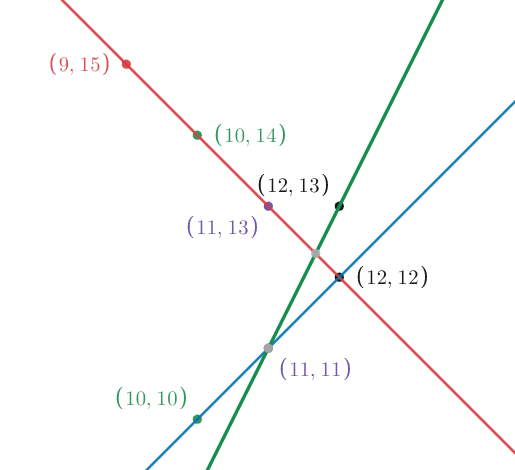
Point (9, 15), (12, 12), (10, 14), (12, 13) lies on one line, point (10, 10), (11, 11), (12 12) lies on another line and lastly point (11, 11), (12, 13) lies on other. So the answer is 3. A little bit of practice can convince you that all the points cannot be covered in less than 3 lines here. So the answer here is 3.
Observation.
- We want to minimize number of lines that covers all the points.
- Any two points can always be connected in a straight line. It is easy to compute if 3 points lie on a line. Let's assume for point A, B and C we want to see if they lie on a line. we can just compute the slope of line segment AB and BC. Equal slope will indicate that they are on the same line.
- It will be helpful for us if we can fit multiple points in a straight line (3 or more).
- We cannot greedily try to fit points. Like, one (incorrect) solution would be: we store all the points in a bag (data stru ture like array or something). In O(n^3) [here n = 16] time we can find out a line that goes through the maximum number of points from the bag, add 1 in our answer (as the number of lines needed till now), remove the points (that are covered by the line) from the bag; we keep repeating this process untill bag is empty. This solution will not work because there can be a better solution if a point lies on a different line (than what we have come up with) and use less number of straight lines. (Think about it).
- Also N = 16 is a good hint for the solution.
Solution approach
- We would like to go through all the solution as greedy does not work. As N = 16, we can use Bitmask DP of O(2^N) to store the state information that will reduce reduntant calculations and make the solution faster.
- Let us use a mask to represent which points (index basically) are already covered till now; value of the corresponding mask will be number of straight lines used.
- In each dp step, we have a mask as state. We can easily find out two points that are not covered by any lines till now; we can add a line between them and also include all the points that lies on that line (We do not need a different line to cover other point(s), think about it). A little bit of hint: we can easily precalculate what other point(s) lie(/s) on the line that connects two certain point on O(n^3) time. [N = 16]
We will again take two uncovered points and repeat the process. Each time we will try to reach the minimum answer possible by the dp. Time complexity here is O(n^2 * 2^n). [n = 16]
Things to apply
Basic geometry, Dynamic programming, Bitmasking
Code in c++
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define pb push_back
#define endl "\n"
#define mp make_pair
const int sz = 17;
bool CHECK(int N,int pos) { return (bool)(N&(1<<pos)); }
unsigned int SET(int N,int pos) { return (N|(1<<pos)); }
int x[sz], y[sz], n, t, tc, dp[1 << sz];
unsigned int sem[sz][sz];
bool semLine(int p1, int p2, int p3){
return x[p1] * y[p2] + x[p2] * y[p3] + x[p3] * y[p1] == x[p2] * y[p1] + x[p3] * y[p2] + x[p1] * y[p3];
}
int go(unsigned int mask){
if(dp[mask] != -1) return dp[mask];
if(mask == (1<<n) - 1) return dp[mask] = 0;
int ans = 8;
int cnt = __builtin_popcount(mask);
if(cnt == n - 1 || cnt == n - 2) return dp[mask] = 1;
for(int i = 0; i < n; i++){
if(CHECK(mask, i)) continue;
for(int j = i + 1; j < n; j++){
if(CHECK(mask, j)) continue;
ans = min(ans, 1 + go(mask | sem[ i ][ j ]));
}
break;
}
return dp[mask] = ans;
}
int main(){
for(scanf("%d", &tc); t < tc; t++){
memset(dp, -1, sizeof dp);
scanf("%d", &n);
for(int i = 0; i < n; i++) scanf("%d %d", x + i, y + i);
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
unsigned int temp = 0;
temp = SET(temp, i);
temp = SET(temp, j);
for(int k = 0; k < n; k++){
if(semLine(i, j, k)) temp = SET(temp, k);
}
sem[i][j] = temp;
}
}
printf("Case %d: %d\n", t + 1, go(0));
}
return 0;
}
Tutorial source



