In short, in this problem, you will be given a positive integer range a to b. You need to output the number of unique Binary Search Tree(BST) can be formed by using the perfect power in that range a to b inclusive.
Binary Search,BST , Catalan Number
Hint
Hint 1
How many perfect power can be found in a range? Is it constant?
Hint 2
How many BST can be formed by using n unique numbers?
Solution
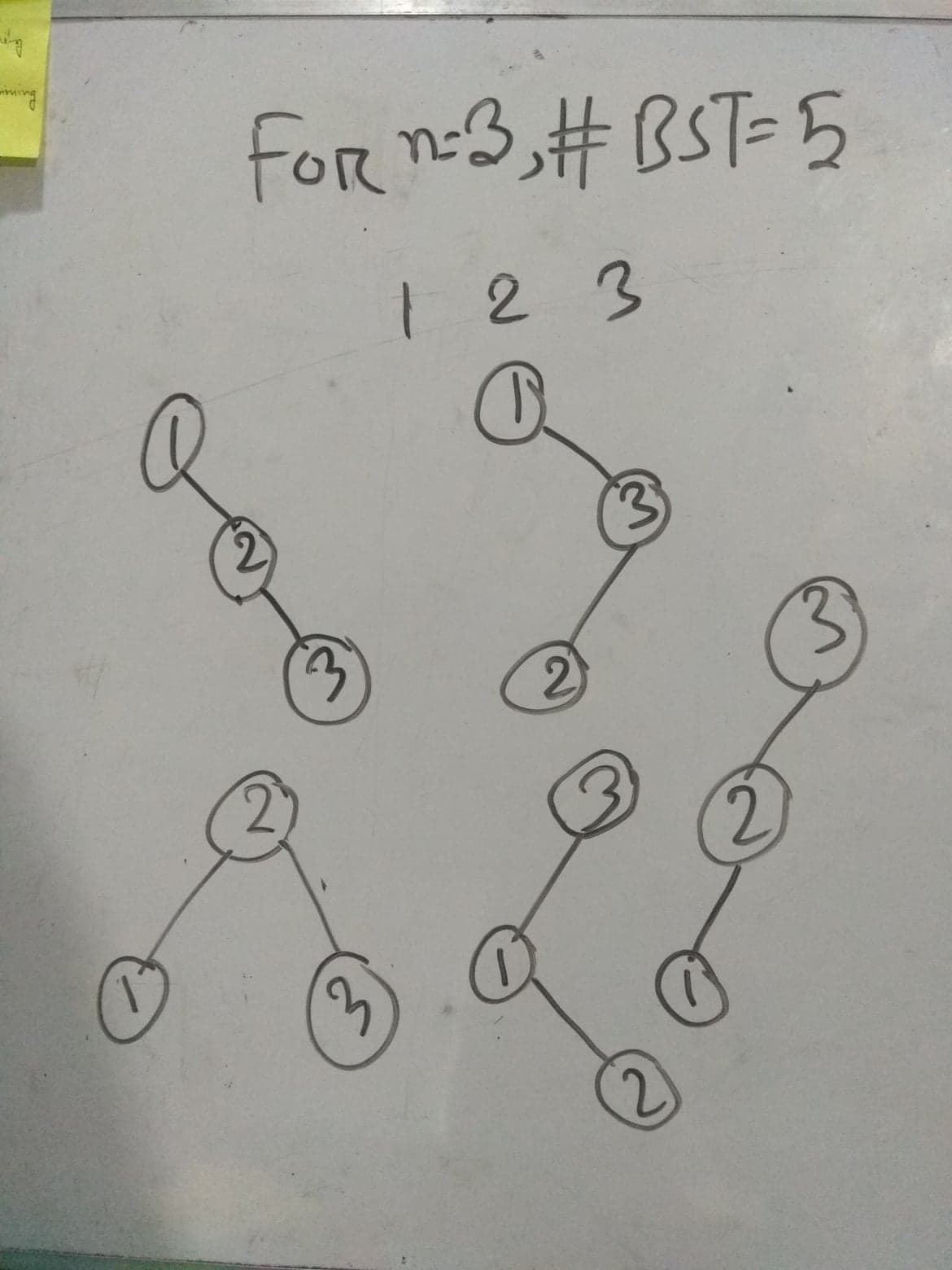
See, in this above example, with 3 different node or key, we can form 5 different BST. Usually, with n different key we can form (2n)! / ((n + 1)! * n!) BST. It is known as Catalan Number as well. First few Catalan Numbers are: for n=0,1,2,3,4...... Cn=1,1,2,5,14..... Again, there is a unique number of perfect power in a range. Thus,our actual problem turns into this:
How many perfect power is there in range a to b?
Since b can be upto 1010,our perfect power can be at most 1000002. We can preprocess all of that necessary perfect power in O(nlogn). Then,we can run binary search to find out the number of perfect power between a to b. You can use lower_bound and upper_bound STL in CPP for that purpose.
Now,we know the number of perfect power in between a to b. Let say, we find n of them.
Then we need , how many BST can be formed by using that n perfect power. We can use this equation (2n)! / ((n + 1)! * n!) or we can use Dynamic Programming(DP).
How does DP work?
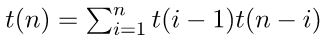
For different value of n,this recurrence relation is true and base case for that recurrence is, for n=0 we can form an empty BST and for n=1 we can form a BST contains a node.
Let say, we have n nodes and if you choose a node as root then we have n-1 non-root node choices. Again,from these n-1 non-root node choices,we can partition them into two parts: one containing the nodes lesser than the root node and one containing the nodes greater than the root. If i is our chosen root node,then we will have i-1 non-root node lesser than root i and n-i non-root node greater than i. For these two sets of non-root node, we will find a certain amount of BST and total BST would be t(i-1)*t(n-i). Multiplication? Because those two non-root set is disjoint. For,choosing every node as root node,we can find total these amount of BST for n nodes.
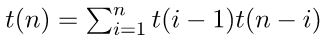
C++
DP
#include<bits/stdc++.h>
using namespace std;
const long long MOD = 100000007;
#define uniq(vec) vec.resize(distance(vec.begin(),unique(vec.begin(),vec.end())))
#define rep(i,a) for(int i=0; i<a;i++)
#define rep1(i,a,b) for(int i=(a);i<=(b);++i)
#define ALL(x) x.begin(),x.end()
#define pb push_back
typedef long long ll;
typedef vector<ll> vll;
const int maxx=100005;
vll pp;
const int maxxn=1150;
ll BST[maxxn];
void solve(){
ll a,b;
cin>>a>>b;
ll n=(upper_bound(ALL(pp),b)-pp.begin())-(lower_bound(ALL(pp),a)-pp.begin());
cout<<BST[n]<<endl;
}
signed main()
{
for(ll i=2;i<=maxx;i++){
ll j=i*i;
while(j<=(ll)1e10){
pp.pb(j);
j*=i;
}
}
sort(ALL(pp));
uniq(pp);
rep(i,maxxn){
if (i==0 || i==1){
BST[i]=1;
}
else{
ll sum =0;ll left, right;
rep1(k,1,i){
left = BST[k-1] % MOD;
right= BST[i-k] % MOD;
sum =(sum%MOD+ (left * right)%MOD)%MOD;
}
BST[i]=sum;
}
}
BST[0]=0;
int t;
cin>>t;
int cs=0;
while(t--){
cout<<"Case "<<++cs<<": ";
solve();
}
return 0;
}
Combinatorics
#include<bits/stdc++.h>
using namespace std;
const long long MOD = 100000007;
#define uniq(vec) vec.resize(distance(vec.begin(),unique(vec.begin(),vec.end())))
#define rep(i,a) for(int i=0; i<a;i++)
#define rep1(i,a,b) for(int i=(a);i<=(b);++i)
#define irep(i,b,a) for(int i=(b);i>=(a);--i)
#define ALL(x) x.begin(),x.end()
#define pb push_back
typedef long long ll;
typedef vector<ll> vll;
const int maxx=100005;
vll pp;
const int maxxn=2*1150;
template<typename T>inline T Bigmod(T base, T power, T MOD){
T ret=1;
while(power)
{
if(power & 1)ret=(ret*base)%MOD;
base=(base*base)%MOD;
power>>=1;
}
return ret;
}
vll fact(maxxn);
void init(){
fact[0]=1;
rep1(i,1,maxxn-1){
fact[i]=(fact[i-1]*i)%MOD;
fact[i]%=MOD;
}
}
void solve(){
ll a,b;
cin>>a>>b;
ll n=(upper_bound(ALL(pp),b)-pp.begin())-(lower_bound(ALL(pp),a)-pp.begin());
if(n==0){
cout<<0<<endl;
return;
}
ll denom=Bigmod((fact[n+1]*fact[n])%MOD,MOD-2,MOD);
ll ans=(fact[2*n]*denom)%MOD;
cout<<ans<<endl;
}
signed main()
{
init();
for(ll i=2;i<=maxx;i++){
ll j=i*i;
while(j<=(ll)1e10){
pp.pb(j);
j*=i;
}
}
sort(ALL(pp));
uniq(pp);
int t;
cin>>t;
int cs=0;
while(t--){
cout<<"Case "<<++cs<<": ";
solve();
}
return 0;
}
Tutorial source

