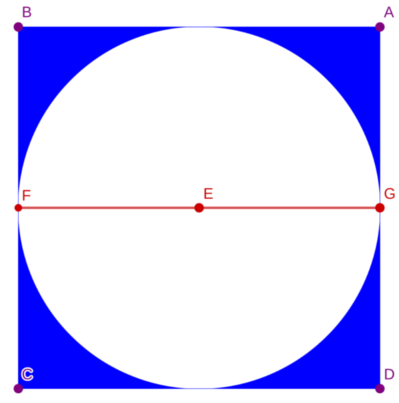
A circle is placed perfectly into a square. The term perfectly placed means that each side of the square is touched by the circle, but the circle doesn't have any overlapping part with the square. See the picture below.

Now you are given the radius of the circle. You have to find the area of the shaded region (blue part). Assume that pi = 2 * acos (0.0) (acos means cos inverse).
Input
Input starts with an integer T (≤ 1000), denoting the number of test cases.
Each case contains a floating point number r (0 < r ≤ 1000) denoting the radius of the circle. And you can assume that r contains at most four digits after the decimal point.
Output
For each case, print the case number and the shaded area rounded to two places after the decimal point.
Sample
| Sample Input | Sample Output |
|---|---|
3 20 30.091 87.0921 | Case 1: 343.36 Case 2: 777.26 Case 3: 6511.05 |
Notes
This problem doesn't have a special judge. So, precision problems could occur. Better to add a small value to your result to avoid this. For example, add 10-9 to your result.
More about rounding errors.